Proof That Each Element of a Topological Space is Contained in Some Component

Theorem

Each element of a topological spaceis contained in some component of

Proof

Obviously each element ofis contained in at least one connected subset of

Letbe the family of all connected subsets ofcontaining

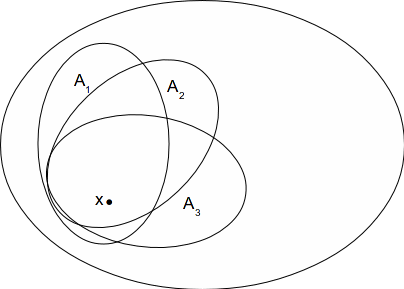
is connected for each

is connected and contains

This union is also unique, since every connected subset ofcontainingis included and non are excluded.

Henceis a maximally connected subset ofcontainingso must be a component of