Proof That Each Element of a Topological Space is Contained in Some Component
Theorem
Each element of a topological space![]() is contained in some component of
is contained in some component of![]()
Proof
Obviously each element of![]() is contained in at least one connected subset of
is contained in at least one connected subset of![]()
Let![]() be the family of all connected subsets of
be the family of all connected subsets of![]() containing
containing![]()
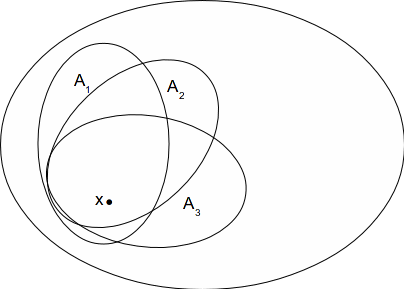
![]() is connected for each
is connected for each![]()
![]() is connected and contains
is connected and contains![]()
This union is also unique, since every connected subset of![]() containing
containing![]() is included and non are excluded.
is included and non are excluded.
Hence![]() is a maximally connected subset of
is a maximally connected subset of![]() containing
containing![]() so must be a component of
so must be a component of![]()