Proof That Every Metric Space is First Countable
Theorem
Every metric space is a first countable space.
Proof
A topological space![]() is first countable if, for each
is first countable if, for each![]() a countable set
a countable set![]() of open sets, each set containing
of open sets, each set containing![]() exists with each open set
exists with each open set![]() containing
containing![]() contains a point of
contains a point of![]() That is,
That is,![]() is first countable if and only if, at every point
is first countable if and only if, at every point![]() a countable local base exists.
a countable local base exists.
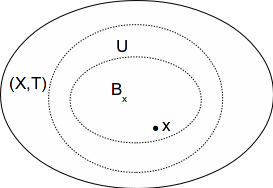
Let![]() be a metric space and let
be a metric space and let![]() The set of open balls
The set of open balls![]()
forms a countable local basis at![]()
For every open set![]() containing
containing![]() a ball
a ball![]() exists.
exists.
Hence every metric space is a first countable space.