Theorem
Let![]() be an open ball in the metric space
be an open ball in the metric space![]() For every point
For every point![]() there exists an open ball
there exists an open ball![]() such that
such that![]()
![]() hence
hence![]()
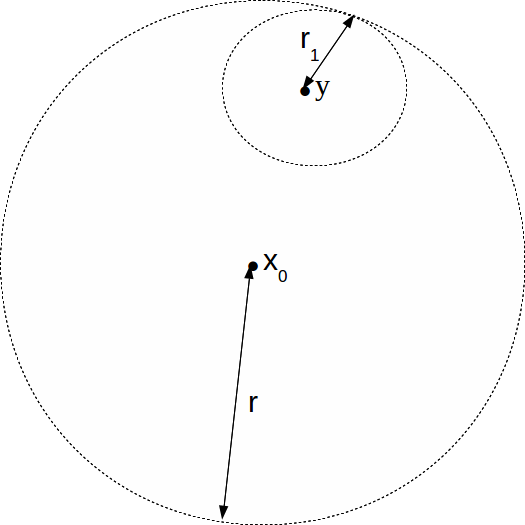
Define![]()
We must show![]()
Suppose![]() then
then![]() or equivalently
or equivalently![]() hence
hence![]()
![]() is a metric so
is a metric so![]()
Hence![]()
Theorem
Let![]() be an open ball in the metric space
be an open ball in the metric space![]() For every point
For every point![]() there exists an open ball
there exists an open ball![]() such that
such that![]()
![]() hence
hence![]()

Define![]()
We must show![]()
Suppose![]() then
then![]() or equivalently
or equivalently![]() hence
hence![]()
![]() is a metric so
is a metric so![]()
Hence![]()