Theorem
If![]() is a separable metric space it is second countable.
is a separable metric space it is second countable.
Proof
Let![]() be a separable metric space. Let A be a countable dense subset of
be a separable metric space. Let A be a countable dense subset of![]() so
so![]()
Let![]() be the set of all open balls with centres in
be the set of all open balls with centres in![]() and with rational radii:
and with rational radii:
![]()
![]() and
and![]() are countable sets, hence so is
are countable sets, hence so is![]()
Take![]() where
where![]() is open in
is open in![]() There is an open ball
There is an open ball![]() such that
such that![]()
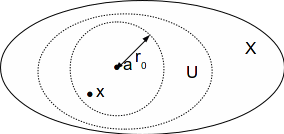
Since![]() is dense in
is dense in![]() we can find
we can find![]() such that
such that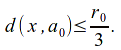
Let![]() be a rational number satisfying
be a rational number satisfying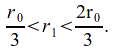
Then![]()
Since![]() and
and![]() is countable,
is countable,![]() is a countable base for the given topology on
is a countable base for the given topology on![]()