Theorem
The first countable property is a topological property.
Proof
Suppose![]() and
and![]() are homeomorphic so that
are homeomorphic so that![]()
Let![]() be a homeomorphism and let
be a homeomorphism and let![]() be first countable. Let
be first countable. Let![]() and let
and let![]() be an open subset of
be an open subset of![]() containing
containing![]()
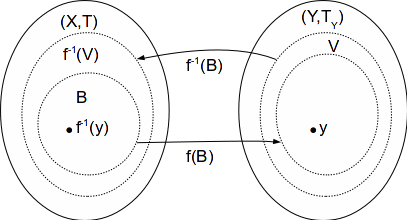
Since![]() is a homeomorphism
is a homeomorphism![]() is a point in
is a point in![]() and
and![]() is an open set in
is an open set in![]() such that
such that![]()
![]() is first countable hence
is first countable hence![]() has a countable local base
has a countable local base![]() An open set
An open set![]() exists such that
exists such that![]() then
then![]() where
where![]() is open in
is open in![]()