Let
be a continuous function.
If
is the restriction of
to
then
is continuous.
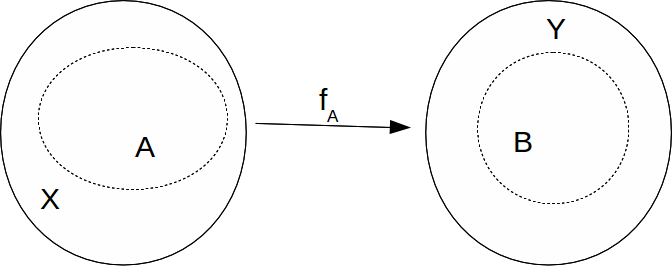
Proof
For any open set
Sinceis continuous
By definition of the induced topology
Hence
and sois continuous.
Letbe a continuous function.
Ifis the restriction oftothenis continuous.
Proof
For any open set
Sinceis continuous
By definition of the induced topology
Henceand sois continuous.