A basis B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. The base 'generates' the topology T. Also
-
The basis elements cover X.
-
Let
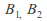 be base elements and let
be base elements and let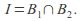 For each
For each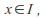 there is a basis element
there is a basis element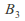 containing
containing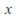 and contained in
and contained in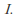 By induction the union of any finite number of basis elements is also a member of the basis.
By induction the union of any finite number of basis elements is also a member of the basis.
If a collection B of subsets of X fails to satisfy either of these, then it is not a base for any topology on X. (It is a subbase, however, as is any collection of subsets of X.) Conversely, if B satisfies both of the conditions 1 and 2, then there is a unique topology on X for which B is a base; it is called the topology generated by B. (This topology is the intersection of all topologies on X containing B.) A sufficient but not necessary condition for B to generate a topology on X is that B is closed under intersections.
For example, the collection of all open intervals in the real line forms a basis for a topology on the real line because the intersection of any two open intervals is itself an open interval or empty. In fact they are a base for the standard topology on the real numbers.
A base is not unique - more than one basis may generate the same topology, even if one basis is a subset of another. For example, the open intervals![]() is a basis for the normal topology on
is a basis for the normal topology on![]() as is the set of open intervals
as is the set of open intervals![]() but these two sets are completely disjoint and both properly contained in the base of all open intervals. A base need not be maximal, but a maximal base exists, given by the topology itself. In fact, any open sets in the space generated by a base may be added to the base without changing the topology.
but these two sets are completely disjoint and both properly contained in the base of all open intervals. A base need not be maximal, but a maximal base exists, given by the topology itself. In fact, any open sets in the space generated by a base may be added to the base without changing the topology.
The set S of all open intervals is a basis for![]() but for example, the set of all semi-infinite intervals of the forms
but for example, the set of all semi-infinite intervals of the forms![]() and
and![]() Then S is not a base for any topology on
Then S is not a base for any topology on![]() since
since![]() is not a semi infinitte interval. One the other hand all semi infinite intervals of the form
is not a semi infinitte interval. One the other hand all semi infinite intervals of the form![]() does form a basis for
does form a basis for![]() The intersection of any finite number of the sets is just the smallest set, and of course
The intersection of any finite number of the sets is just the smallest set, and of course![]() 2. is obviously satisfied.
2. is obviously satisfied.