The Four Colour Mapping Theorem
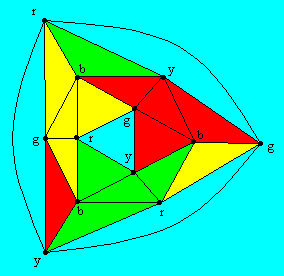
How many different colors are sufficient to color the countrieson a map in such a way that no two adjacent countries have thesame color? The figure below shows a typical arrangement ofcoloured regions.

Notice that we define adjacent regions as those that share acommon boundary of non-zero length. Regions which meet at a singlepoint are not considered to be "adjacent".
After examining a wide variety of different planar graphs, onediscovers the apparent fact that every graph, regardless of sizeor complexity, can be colored with just four distinct colors. This"four-color conjecture" was first noted by AugustFerdinand Mobius in 1840. In 1852 a young man named FrancisGuthrie wrote about the problem in a letter to his brotherFrederick, then a student at University College in London. Neitherof the brothers was able to prove the conjecture, so Frederickasked one of his professors, Augustus DeMorgan (1806-1871).DeMorgan too was unable to prove the conjecture, and afterrecognizing the difficulty of the problem, he wrote to Sir WilliamRowan Hamilton (1805-1865) to ask for help. It might seem thatthis problem would be irresistible to Hamilton, since anythinghaving to do with the number "four" immediately suggestsa connection with his beloved quaternions. Also, Hamilton madecontributions to graph theory (such as the idea of a Hamiltoniancircuit, i.e., a path along the edges of a graph that visits eachvertex exactly once), a subject that was developed largely throughefforts to prove the four color conjecture. Nevertheless, Hamiltonimmediately wrote back that he did not believe he would solveDeMorgan's "quaternion of colors" any time soon.
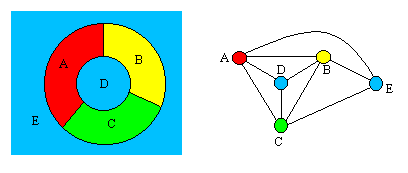
The coloring of geographical maps is essentially a topologicalproblem, in the sense that it depends only on the connectivitiesbetween the countries, not on their specific shapes, sizes, orpositions. We can just as well represent each country by a singlepoint (vertex), and the adjacency between two bordering countriescan be represented by a line (edge) connecting those two points.It's understood that connecting lines cannot cross each other. Adrawing of this kind is called a planar graph. A simple map (withjust five "countries") and the corresponding graph areshown below.
A graph is said to be n-colorable if it's possible to assignone of n colors to each vertex in such a way that no two connectedvertices have the same color. Obviously the above graph is not3-colorable, but it is 4-colorable. The Four Color Theorem assertsthat every planar graph - and therefore every "map" onthe plane or sphere - no matter how large or complex, is4-colorable. Despite the seeming simplicity of this proposition,it was only proven in 1976, and then only with the aid ofcomputers.
Notice that the above graph is "complete" in thesense that no more connections can be added (without crossinglines). The edges of a complete graph partition the graph planeinto three-sided regions, i.e., every region (including theinfinite exterior) is bounded by three edges of the graph. Everygraph can be constructed by first constructing a complete graphand then deleting some connections (edges). Clearly the deletionof connections cannot cause an n-colorable graph to require anyadditional colors, so in order to prove the Four Color Theorem it
Although DeMorgan was unable to prove the four-colorconjecture, he did observe that no more than four regions on theplane can all be in mutual contact with each other. The graph of aset of three mutually adjoining regions is simply a topologicaltriangle, and if we add a fourth region, it is represented by afourth vertex in the graph, which must be located either inside oroutside the triangle formed by the graph of the original threevertices. In either case, we must then connect this fourth vertexwith each of the three original vertices so that all four of theregions are mutually adjoining. Having done this, we can slide thevertices around (if necessary) to bring the graph into the formshown below.
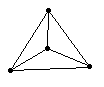
This is the unique graph of four mutually adjoining planeregions (V = 4, E = 6), and also of the tetrahedron. It clearlydivides the graph plane into four isolated regions, one regionexterior to the big triangle, and the three interior regions. Afifth vertex added to this graph will be able to have edges thatreach only three of the four existing vertices, because each ofthe four regions is completely bounded by three edges that blockaccess to one of the existing vertices. Hence there does not exista plane graph of five mutually connected vertices, so there does
Of course, the non-existence of a graph with five mutuallyadjoining vertices does not automatically imply the non-existenceof a graph requiring five distinct colors. For example, thereexist graphs in which the largest subset of mutually adjoiningvertices is two, and yet for which three colors are required. Thisis the case with any simple loop with an odd number of vertices,as illustrated in the left-hand figure below. Similarly there aregraphs containing no subset of four mutually adjoining verticesthat nevertheless require four colors, such as the graph shown on
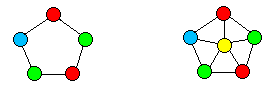
Therefore, we must consider the possibility that five colorsmight be required for some graph, even though it's not possiblefor a graph to contain any set of five mutually connectedvertices.
On the other hand, it could be argued that the two exampleshown above can each be reduced, clarifying the causal linksbetween different parts of the graphs. For example, in the leftfigure we have an alternating sequence of red, green, red, green,and if these were the only two available colors, it's clear thatthe chain must continue to alternate, no matter how long - or howshort. Thus we could just as well replace any chain of the formrgrg...rg with the simple pair rg, in which case the left-handfigure above consists of three mutually connected vertices.Likewise if we replace the circumferential chain rgrg around thecentral yellow vertex in the right hand figure with just the pair
In view of this, it's tempting to think that DeMorgan'sobservation somehow, perhaps indirectly, does ultimately accountfor the truth of the four-color theorem. Indeed if we construct agraph by adding vertices, one at a time, and make the maximumnumber of connections at each stage, we will always find the graphplane divided into "triangular" regions, each of whichhas access to only three vertices. Thus it follows that fourcolors suffice for any graph that can be constructed in this way.For example, consider the two graphs shown below.
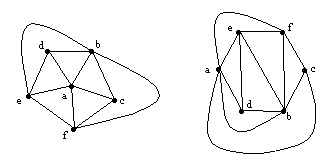
These two graphs each have V = 6 vertices and E = 12 edges, andin fact the two graphs are topologically identical. The planeregions represented by the vertices "a" and "b"each have five adjoining neighbors, whereas the vertices "e"and "f" each have four, and the vertices "c"and "d" each have three. These are complete graphs and,as noted above, a complete graph divides the entire graph planeinto "triangular" regions, i.e., regions bounded bythree edges connecting three vertices. Nevertheless, depending onhow we add the points, it is possible that when a vertex is addedto a graph it has more than three neighbors, so we cannot sayautomatically that four colors would suffice. For example, ifvertex "a" is the last to be added, it would have fivepre-existing neighbors, and if four colors have already been usedin those five vertices, the vertex "a" would require afifth color.
However, we need not add vertex "a" last. Anothertopologically equivalent way of drawing the above graph is shownbelow.
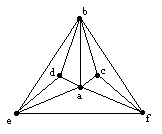
This shows that we could first assign three distinct colors tothe vertices e,b,f, and then place the vertex "a" inthis triangle, connect it to each of the three surroundingvertices, and give it a fourth color. Then we can place vertex dinside the triangle abe and give it the same color as f. Then wecan place vertex c inside the triangle abf and give it the colorof e. Hence the graph is 4-colorable. Moreover, any graph, orportion of a graph bounded by a triangle such as ebf , and havingthis hierarchical pattern of nested triangles, is 4-colorable.This is the case when the graph contains some vertices with onlythree edges, and when those vertices and edges are removed, theremaining graph has some vertices with only three edges, which canbe removed, and so on, until finally all that remains is a singletriangle.
Unfortunately (for the prospect of a simple proof), not everygraph is of this hierarchical form. For example, consider thecomplete graph shown below.
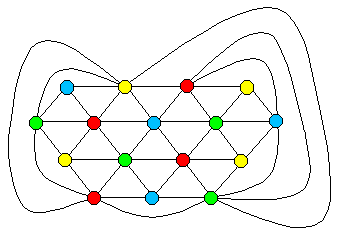
This graph has V = 16 vertices and E = 42 edges. It is nothierarchical, because after removing the two vertices having onlythree edges each, the remaining graph has four or more edgesattached to each vertex. (We can also infer that this graph is nothierarchical from the fact that no three mutually connectedvertices are directly connected to a fourth vertex.) Nevertheless,this graph is 4-colorable, as shown in the figure.
The above graph contains a "flat" patch consisting ofa uniform hexagonal grid. An infinite hexagonal grid is obviously4-colorable by means of the alternating layered pattern shownbelow.
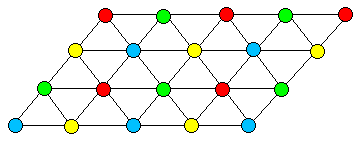
In a sense, two extreme types of graph structures are thepurely hierarchical graphs and the perfectly "flat"graphs, both of which are easily seen to be 4-colorable.
Notice that we need not consider graphs containing anyconfigurations of four mutually connected vertices, because, asdiscussed previously, the edges of such a configurationnecessarily split the graph plane into four separate regions, eachof which has access to only three of the four vertices. Hence ifwe can 4-color the interior of such a triangle, we can 4-color thetetrahedral "frame" as well. If we could reduce all thecausal links in a graph to their bare minimums, it might bepossible to reduce every n-colorable graph to a graph with just nmutually connected vertices, and hence n could never exceed four.However, the reduction of graphs with more than two colors is nota trivial task.
If we denote the number of vertices, edges, and faces (i.e.,the bounded regions) of a planar graph by V, E, and Frespectively, then Euler's formula for a plane (or a sphere) is V- E + F = 2. Furthermore, each face of a complete graph is boundedby three edges, and each edge is on the boundary of two faces, sowe have F = 2E/3, and Euler's formula for a complete planar graphis simply E = 3V - 6. Now, each edge is connected to two vertices,so the total number of attachments (in a complete graph) is 2E =6V - 12, and hence the average number of attachments per vertex is6 - 12/V. For any incomplete graph, the total number ofattachments is less. Consequently the average number ofattachments per vertex for any graph (with a finite number ofvertices) is less than 6, which implies that at least one vertexhas only five or fewer attachments.
If we have six available colors, a vertex with only fiveneighbors obviously imposes no constraint on the coloring of theother vertices, because, regardless of the colors of its five (orfewer) neighbors, we can assign it a color without exceeding thesix available colors. Therefore if we delete this vertex and allits connections from the graph, creating a graph with one fewervertices, it's clear that if the resulting graph is 6-colorable,then so was the original graph. Moreover, Euler's formula assuresus that this reduced graph also contains at least one vertex withfive or fewer neighbors, so we can apply this procedurerepeatedly, reducing the graph eventually to one with just 6vertices, which is obviously 6-colorable. Hence the original graphis 6-colorable.
So, we've seen that Euler's formula immediately implies that nograph can require more than six colors. Furthermore, with just alittle more work, we can also show that no graph can require morethan five colors. (Ultimately we will see that no graph canrequire more than four colors, but it's worthwhile to begin withthe proof of the 5-colorability of every planar graph.) Obviouslyevery graph with five or fewer vertices is 5-colorable, so ifthere exists a finite graph that requires more than five colors,it must have more than five vertices. Let the positive integer V6denote the smallest number of vertices on which there exists agraph that requires six (or more) colors. Conversely, every graphwith fewer than V6 vertices is 5-colorable.
Now, assuming the existence of a graph that requires more thanfive colors, we can consider one that has exactly V6 vertices. ByEuler's formula, this graph must contain at least one vertex withfive or fewer connections. However, it cannot contain any vertexwith just four (or fewer) connections, because if it did, we coulddelete such a vertex and leave a graph with just V6 - 1 vertices,which is 5-colorable by definition. Re-inserting the deletedvertex would clearly have no effect on the 5-colorability of thegraph, because the vertex has only four (or fewer) neighbors, sothe original graph must be 5-colorable, contradicting ourassumption. Therefore, a graph with V6 vertices that requires morethan five colors cannot contain any vertex with just four or fewerneighbors.
Since Euler's formula implies that the graph contains at leastone vertex with five or fewer connections, the only remainingpossibility is that the graph contains a vertex with exactly fiveconnections. However, this too leads to a contradiction. To showthis, it's helpful to introduce the notion of a k-cluster, whichis specified by a set of k distinct colors and one particularvertex that has one of those colors. The original vertex isincluded in the cluster, and, in addition, every vertex with oneof the k specified colors that neighbors a vertex in the clusteris also in the cluster. By definition the only vertices outside acluster that are directly connected to vertices inside the clusterhave colors that are not in the specified set of k colors.Therefore, we can apply any permutation of the k colors to thevertices in a cluster without invalidating the coloration. Inparticular, a 2-cluster is a contiguous set of vertices, each withone of two specified colors, and we can transpose these two colorswithout upsetting the coloration of a graph.
Now consider a graph containing a vertex with exactly fiveimmediate neighbors, of five distinct colors, as illustratedbelow.
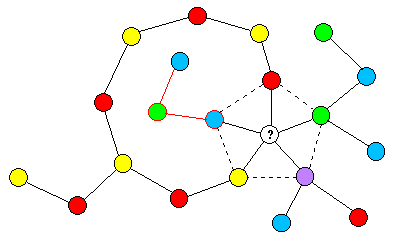
Since the uncolored vertex in the center has neighbors of fivedistinct colors, it might seem that a sixth color is required.However, notice that we can transpose the blue and green colors inthe blue/green 2-cluster attached to the upper left vertex of thecentral pentagon, so that the upper left vertex is green insteadof blue. Once we have done this, the uncolored vertex in thecenter has neighbors of only four distinct colors. If we deletethe central vertex, the overall graph has V6 - 1 vertices, so itis 5-colorable, but re-inserting this vertex requires no sixthcolor (once we have transposed the blue and green in the small2-cluster as described), so the original graph is 5-colorable.
The only possible objection to the transposing of the colors ina cluster as a means of reducing the number of distinct colorsaround the perimeter of the pentagon is that we cannot necessarilychange the color of any vertex to the color of one of the oppositevertices of the pentagon, because two opposite vertices of apentagon might be in the same 2-cluster. This is the case, forinstance, with the yellow and red vertices of the pentagon in thefigure above. If we transpose the red and yellow colors in this2-cluster, there would still be five distinct colors around theperimeter of the pentagon. However, if such a cluster exists,connecting two opposite vertices of the pentagon, we areguaranteed that at least one other pair of vertices are cut offfrom each other, i.e., they cannot be in the same 2-cluster. Forexample, the blue/green 2-cluster outlined in red in the abovefigure cannot be part of the blue/green 2-cluster attached to theupper right of the pentagon. In general, for any vertex connectedto exactly five other vertices, we can always (withoutinvalidating the coloration) change the color of at least one ofthe five neighbors so that there are only four distinct colors. Itfollows, using the reduction argument described in the precedingparagraph, that no graph can require more than five colors.
This still leaves open the question of whether five colors areever actually required, or whether four colors will alwayssuffice. If there exist planar graphs requiring five distinctcolors, there must be a positive integer V5 that is the smallestnumber of vertices on which such a graph can be constructed. Let'scall a graph with V5 vertices that requires five colors a minimal5-color graph. By the reduction argument described previously,such a graph obviously cannot contain any vertex with three orfewer connections. Moreover, by considering 2-clusters again, wecan prove that such a graph cannot contain any vertex with justfour connections. To see why, consider the portion of a graphillustrated below.
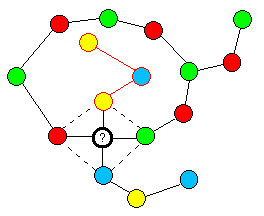
The uncolored vertex in the center has just four neighbors,which we've colored red, yellow, green, and blue. This might seemto require a fifth color for the central vertex, but in fact bypermuting the yellow and blue colors in the 2-cluster (outlined inred) above the central vertex we can transform this coloration sothat the central uncolored vertex has neighbors of only threedistinct colors (red, green, and blue). Since the overall graphfrom which this configuration was taken is assumed to have exactlyV5 vertices, it follows that if we delete the central vertex, theresulting graph has only V5 - 1 vertices, so it is 4-colorable,but we can clearly add the central vertex back without requiring afifth color, so the whole graph must be 4-colorable, contradictingour original assumption. This shows that it's always possible tomodify a graph containing a vertex with only four connections insuch a way that the vertex is connected to only three distinctcolors. At most, only one of the two pairs of opposite verticescan be linked by a common 2-cluster, because if one pair is solinked, the other cannot be linked.
To summarize the argument up to this point, we've shown that nograph can require more than five colors, and we've also shown thatif there exists a graph requiring five colors, there must exist aminimal 5-color graph, and such a graph cannot contain any vertexwith fewer than five connections. Also, by adding connections, wecan "complete" any graph on V vertices so that all thefaces are triangular and there are a total of exactly 6V-12attachments. This graph must still be a minimal 5-color graphbecause we haven't increased the number of vertices, and addingconnections cannot reduce the number of colors required, whereasno graph requires more than five colors. Therefore, letting a5,a6, a7,... denote the number of vertices with precisely 5, 6,7,... attachments respectively, we must have a minimal 5-colorgraph such that
![]()
where V = a5 + a6 + a7 + a8 + a9 + ... Substituting thisexpression for V into the above formula and re-arranging, we havethe condition
![]()
This places fairly severe constraints on any putative completeminimal 5-color graph. For example, if we consider only suchgraphs with no more than six attachments at any single vertex,then this formula implies a5 = 12. In other words, a completeminimal 5-graph with no more than six attachments per vertex musthave exactly 12 vertices with five attachments each. This suggeststhat these 12 vertices are arranged globally in the pattern of anicosahedron, and the remaining vertices with six attachments pervertex are in a regular hexagonal pattern, filling in the "faces"of the icosahedron. (This pattern is the basis for "geodesicdomes"). The fundamental graph of this type, with a6 = 0, isshown below.
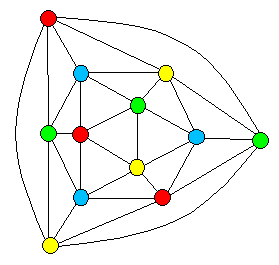
We can give explicit 4-colorings of every such pattern, so suchgraphs can be shown explicitly to require no more than fourcolors. Therefore, if a complete minimal 5-color graph exists, itmust contain at least one vertex with seven or more attachments.
It was not until 1976 that, with the help of modern computers,the 4-color conjecture was finally proven to be true. The proof,developed by Appel and Haken based on ideas of several earlierpeople (Kempe, Heawood, Birkhoff, etc) consisted of finding a setof subgraphs, at least one of which must be contained in anynormal planar graph (i.e., the set is unavoidable), and such thatif a graph containing one of those sub-graphs is not 4-colorable,then neither is a graph with one fewer vertices. This leadsimmediately to a contradiction, because it implies that, if wehypothesize the existence of a graph that is not 4-colorable, wecan always construct another graph, with fewer vertices, that isalso not 4-colorable, eventually arriving at a graph with onlyfour vertices, but this graph obviously is 4-colorable. Hence wehave a contradiction, so we can conclude that the originalhypothesis was false, i.e., there does not exist a graph that isnot 4-colorable. The unavoidable set found by Appel and Hakenconsisted of nearly 1500 subgraphs, and many of these requiredconsiderable analysis to prove that they were "reducible".The development of this unavoidable set, and the proofs ofreducibility for its members, was carried out largely oncomputers, so the proof is notable (and slightly controversial) asan early example of a mathematical proposition whose proof canonly be carried out on a computer, and is, in some sense, beyondhuman mental capabilities to verify.
It's interesting to consider the problem of determining a4-coloring for any given graph from a purely algebraic standpoint(harking back to Hamilton's quaternions). We might stipulate thateach vertex is to be assigned one of four possible values, and theconditions imposed by the connections would be represented byalgebraic equations, one equation for each connection. Part of thedifficulty of this approach is that the condition of adjacency isnot an equality, it is an inequality, i.e., we require that twovertices have unequal values (from among the four possiblevalues). Also, there is necessarily a great deal of ambiguity inthe solution, because any permutation of the colors leaves asolution intact. In addition, there is even more ambiguity, sincein general there can be more than one distinct 4-coloration of agraph.
Given the four allowable (distinct) values a,b,c,d, we couldalgebraically impose the requirement for every vertex to have oneof these values by requiring that the value u assigned to anyvertex satisfies f(u) = 0, where the polynomial f is defined as
![]()
Then we could algebraically impose the required inequality onthe values u,v assigned to two connected vertices by stipulatingthat g(uv) = 0, where the polynomial g is defined as
![]()
The equation g(uv) = 0 is satisfied if and only if u and v havedistinct values from the set {a,b,c,d}. For example, the set{-2,-1,1,2} gives
![]()
To illustrate, consider again the octahedral graph (which is 3-colorable):
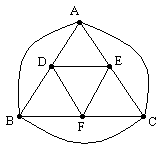
The algebraic conditions for the individual "color"values assigned to the six variables A,B,C,D,E,F are
![]()
and the algebraic conditions imposed by the twelve connectionsare
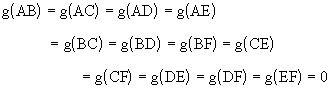
This amounts to 18 equations in the 6 variables. We can,however, without loss of generality stipulate the "colors"of three of the variables, say, A = 1, B = -1, C = 2, since thesethree must have mutually distinct values. This leaves us with thefollowing twelve equations in the three unknowns D,E,F
![]()
and
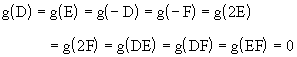
The three equations f(D) = 0, g(D) = 0, and g(-D) = 0 jointlyhave only two solutions, namely, D = 2 and D = -2. Therefore thosethree equations can be replaced with the single equation D2 - 4 =0. Likewise the three equations involving only E can be reduced toE2 + 3E + 2 = 0, and the three equations involving only F can bereduced to F2 + F - 2 = 0. Thus we have six equations in the threeunknowns.
A different approach would be to assign a four-dimensionalvector to each vertex, and then the connection between two givenvertices would be represented by requiring the dot product ofthose two vectors to vanish, i.e., requiring that the two vectorsbe mutually orthogonal. The three vectors assigned to the verticesof any triangle would then be an orthogonal triad with someorientation in 4-dimensional space. Likewise the four vectorsassigned to the vertices of a tetrahedral graph would be acomplete set of four mutually orthogonal vectors (a tetrad), butstill with arbitrary orientation. For example, the conditions onthe six vectors A,B,C,D,E,F assigned to the vertices of theoctahedral graph shown above would be simply
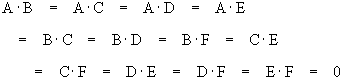
In this context the four color theorem tells us that a space offour dimensions is sufficient to enable us to assign one of thefour basis vectors to each vertex of a planar graph in such a waythat the vectors of every pair of adjacent vertices areorthogonal. We can assume each vector is of unit length, so it hasthree independent components. Therefore, we have 18 independentcomponents in all, constrained by 12 equations. Naturally thesystem is underspecified, because we can apply an arbitrarypermutation to the vectors.
Since the edges of a complete graph partition the graph planeinto three-sided regions whose vertices are three mutuallyconnected points, we can uniquely assign the fourth color to eachof these regions. The result is useful for visualizing thesymmetries of the coloring. For example, the 4-colored icosahedralgraph discussed above looks like this: