Proof
Let![]() be a set and let
be a set and let![]() be a family of subsets of
be a family of subsets of![]() so that
so that![]() the discrete topology. There is a unique smallest topology
the discrete topology. There is a unique smallest topology![]() such that
such that![]() given by
given by![]()
![]() is said to be generated by A.
is said to be generated by A.
Proof
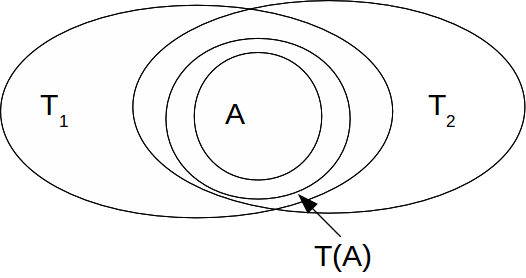
Let![]() and let
and let![]() be the intersection of all topologies
be the intersection of all topologies![]() containing
containing![]()
![]() is a topology since
is a topology since
1.![]() for each
for each![]() so
so ![]()
2. If![]() for each
for each![]() then
then![]() for each
for each![]() so
so ![]()
2. If![]() for each
for each![]() then
then![]() for each
for each![]() so
so![]()
Since![]() is the intersection of all the topologies containing
is the intersection of all the topologies containing![]() it must be the smallest topology containing
it must be the smallest topology containing![]() If there is any other smallest topology
If there is any other smallest topology![]() then
then![]() is a smaller topology than either
is a smaller topology than either![]() or
or![]() containing A - a contradiction - so
containing A - a contradiction - so![]() is unique.
is unique.
Also since![]() and
and![]() is a topology, it must contain all intersections and unions of elements of
is a topology, it must contain all intersections and unions of elements of![]()