A Lie group is simultaneously a group and a smooth manifold e.g.![]() or a circle - which is a specific kind of geometric object. The circle and the sphere are examples of smooth manifolds. Finally the algebraic structure and the geometric structure must be compatible in a precise way.
or a circle - which is a specific kind of geometric object. The circle and the sphere are examples of smooth manifolds. Finally the algebraic structure and the geometric structure must be compatible in a precise way.
Informally, a Lie group is a group of symmetries where the symmetries are continuous. The symmetries of a circle are the rotations and reflections in a line through the origin together with the identity and inversion. The rotations may be continuously deformed onto each other within the group, and so might the reflections. This is in contrast with the triangle, which has only three distinct rotations and three distinct reflections.
Lie groups were introducing in the solving of equations. There are many techniques for solving equations, one of which is to make a change of variables which makes the equation simpler and easier to solve, with maybe one variable dropping out of the equations. This occurs because of an underlying symmetry of the equations, and underlying this symmetry is a Lie Group.
Examples:
-
Euclidean space
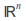 with ordinary vector addition as the group operation.
with ordinary vector addition as the group operation.
-
The circle group
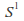 consisting of rotations
consisting of rotations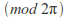 under addition.
under addition. -
The group
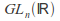 of invertible matrices (under matrix multiplication) is a Lie group of dimension
of invertible matrices (under matrix multiplication) is a Lie group of dimension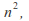 called the general linear group. It has a closed connected subgroup
called the general linear group. It has a closed connected subgroup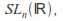 the special linear group, consisting of matrices of determinant 1 which is also a Lie group.
the special linear group, consisting of matrices of determinant 1 which is also a Lie group. -
The orthogonal group
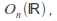 consisting of all
consisting of all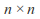 orthogonal matrices with real entries is an
orthogonal matrices with real entries is an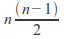 - dimensional Lie group. This group is disconnected, but it has a connected subgroup
- dimensional Lie group. This group is disconnected, but it has a connected subgroup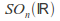 of the same dimension consisting of orthogonal matrices of determinant 1, called the special orthogonal group (for
of the same dimension consisting of orthogonal matrices of determinant 1, called the special orthogonal group (for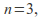 the rotation group).
the rotation group). -
The unitary group
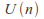 consisting of
consisting of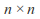 unitary matrices (with complex entries) is a compact connected Lie group of dimension
unitary matrices (with complex entries) is a compact connected Lie group of dimension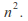 Unitary matrices of determinant 1 form a closed connected subgroup of dimension
Unitary matrices of determinant 1 form a closed connected subgroup of dimension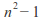 denoted
denoted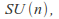 the special unitary group.
the special unitary group. -
Spin groups are double covers of the special orthogonal groups, used for studying fermions in quantum field theory (among other things).
-
The symplectic group
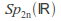 consisting of all
consisting of all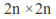 matrices preserving a nondegenerate skew-symmetric bilinear form on
matrices preserving a nondegenerate skew-symmetric bilinear form on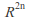 (the symplectic form). It is a connected Lie group of dimension
(the symplectic form). It is a connected Lie group of dimension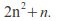
-
The 3-sphere
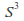 forms a Lie group by identification with the set of quaternions of unit norm, called versors. The only other spheres that admit the structure of a Lie group are the 0 - sphere
forms a Lie group by identification with the set of quaternions of unit norm, called versors. The only other spheres that admit the structure of a Lie group are the 0 - sphere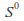 (real numbers with absolute value 1) and the circle
(real numbers with absolute value 1) and the circle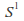 (complex numbers with absolute value 1).
(complex numbers with absolute value 1).