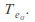Every Lie Group![]() has an associated Lie algebra whose underlying vector space is the tangent space of G at the identity element, which completely captures the local structure of the group. We can think of elements of the Lie algebra as elements of the group that are "infinitesimally close" to the identity, and the Lie bracket is the commutator of two such infinitesimal elements if G is a matrix group.
has an associated Lie algebra whose underlying vector space is the tangent space of G at the identity element, which completely captures the local structure of the group. We can think of elements of the Lie algebra as elements of the group that are "infinitesimally close" to the identity, and the Lie bracket is the commutator of two such infinitesimal elements if G is a matrix group.
-
The Lie algebra of the vector space
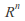 is just
is just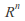 with the Lie bracket given by
with the Lie bracket given by
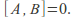 (In general the Lie bracket of a connected Lie group is always 0 if and only if the Lie group is abelian.)
(In general the Lie bracket of a connected Lie group is always 0 if and only if the Lie group is abelian.)
-
The Lie algebra of the general linear group
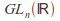 of invertible matrices is the vector space
of invertible matrices is the vector space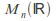 of square matrices with the Lie bracket given by
of square matrices with the Lie bracket given by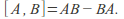
Example:
If![]() is a closed subgroup of
is a closed subgroup of![]() then the Lie algebra of
then the Lie algebra of![]() can be thought of informally as the matrices
can be thought of informally as the matrices![]() of
of![]() such that
such that![]() is in
is in![]() where
where![]() is infinitesimally small so that
is infinitesimally small so that![]() For example, the orthogonal group
For example, the orthogonal group![]() consists of matrices
consists of matrices![]() with
with![]() so the Lie algebra consists of the matrices
so the Lie algebra consists of the matrices![]() with
with![]() which is equivalent to
which is equivalent to![]() because
because![]()
Not all Lie groups can be represented in terms of matrices, so the general definition of the Lie algebra of any Lie group is given by the following steps:
1. Vector fields on any smooth manifold![]() can be thought of as derivatives
can be thought of as derivatives![]() of the ring of smooth functions on the manifold, and therefore form a Lie algebra under the Lie bracket
of the ring of smooth functions on the manifold, and therefore form a Lie algebra under the Lie bracket![]() because the Lie bracket of any two derivations is a derivation.
because the Lie bracket of any two derivations is a derivation.
2. If![]() is any group acting smoothly on the manifold
is any group acting smoothly on the manifold![]() then it acts on the vector fields, and the vector space of vector fields fixed by the group is closed under the Lie bracket and therefore also forms a Lie algebra.
then it acts on the vector fields, and the vector space of vector fields fixed by the group is closed under the Lie bracket and therefore also forms a Lie algebra.
3. We apply this construction to the case when the manifold![]() is the underlying space of a Lie group
is the underlying space of a Lie group![]() with
with![]() acting on
acting on![]() by left translations
by left translations![]() This shows that the space of left invariant vector fields (vector fields satisfying
This shows that the space of left invariant vector fields (vector fields satisfying![]() for every
for every![]() where
where![]() denotes the differential of
denotes the differential of![]() ) on a Lie group is a Lie algebra under the Lie bracket of vector fields.
) on a Lie group is a Lie algebra under the Lie bracket of vector fields.
4. Any tangent vector at the identity of a Lie group can be extended to a left invariant vector field by left translating the tangent vector to other points of the manifold. Specifically, the left invariant extension of an element![]() of the tangent space at the identity is the vector field defined by
of the tangent space at the identity is the vector field defined by![]() This identifies the tangent space
This identifies the tangent space![]() at the identity with the space of left invariant vector fields, and therefore makes the tangent space at the identity into a Lie algebra, called the Lie algebra of G,
at the identity with the space of left invariant vector fields, and therefore makes the tangent space at the identity into a Lie algebra, called the Lie algebra of G,
This Lie algebra is finite-dimensional and it has the same dimension as the manifold G. The Lie algebra of G determines G up to "local isomorphism", where two Lie groups are called locally isomorphic if they look the same near the identity element. Problems about Lie groups are often solved by first solving the corresponding problem for the Lie algebras, and the result for groups then usually follows easily. For example, simple Lie groups are usually classified by first classifying the corresponding Lie algebras.
We can also define a Lie algebra structure on![]() using right invariant vector fields instead of left invariant vector fields. This leads to the same Lie algebra, because the inverse map on G can be used to identify left invariant vector fields with right invariant vector fields, and acts as the inverse on the tangent space
using right invariant vector fields instead of left invariant vector fields. This leads to the same Lie algebra, because the inverse map on G can be used to identify left invariant vector fields with right invariant vector fields, and acts as the inverse on the tangent space![]()
The Lie algebra structure on![]() can also be described as follows: the commutator operation
can also be described as follows: the commutator operation
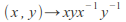 on
on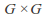 sends
sends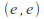 to
to so its derivative yields a bilinear operation on
so its derivative yields a bilinear operation on