Dielectric may not be neutral even when unpolarised. If the dielectric carries a charge density![]() of free charges representing a net surplus or deficit of electrons in the atoms of the dielectric and
of free charges representing a net surplus or deficit of electrons in the atoms of the dielectric and![]() is the charge density due to the polarizing effect of an electric field then the total charge density is given by
is the charge density due to the polarizing effect of an electric field then the total charge density is given by![]()
The macroscopic electric field![]() is related to the total charge density, and in the presence of matter Gauss's Law becomes
is related to the total charge density, and in the presence of matter Gauss's Law becomes
![]()
We can rearrange this expression to give![]() If we define
If we define![]() then this equation becomes
then this equation becomes![]()
![]() is a new vector field, called the electric displacement. Since
is a new vector field, called the electric displacement. Since![]() we can write
we can write![]()
The last equation is really Gauss's Law, apart from a constant factor, modified to include polarization charges. This can be further illustrated using the integral form of Gauss's Law:
![]()
which becomes![]() on substituting (1).
on substituting (1).
![]() has no clear meaning, but is useful because it makes many problems very easy to solve. It has the property that the normal component of
has no clear meaning, but is useful because it makes many problems very easy to solve. It has the property that the normal component of![]() at a dielectric boundary is continuous, as illustrated in the diagram below.
at a dielectric boundary is continuous, as illustrated in the diagram below.
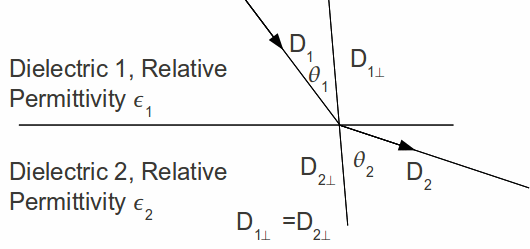
![]() so
so![]()