Perturbed and unperturbed phase curves of a Hamiltonian system can be connected via a canonical transformation. This suggest that perturbation theory for Hamiltonian systems is really the study of canonical transformation which depend upon a parameter![]() which form a family of transformations which reduce to the identity when
which form a family of transformations which reduce to the identity when![]() Generating functions are really not suitable here because they are functions of both new and old coordinates and give implicit expressions for the coordinates. For most purposes we need the old coordinates as functions of the new coordinates.
Generating functions are really not suitable here because they are functions of both new and old coordinates and give implicit expressions for the coordinates. For most purposes we need the old coordinates as functions of the new coordinates.
Consider those canonical transformations![]() which are close to the identity transformation:
which are close to the identity transformation:![]()
This has the generating function![]() so a Hamiltonian is perturbed slightly:
so a Hamiltonian is perturbed slightly:![]() where
where![]() is a small parameter, we would expect a transformation close to the identity:
is a small parameter, we would expect a transformation close to the identity:![]() to have a generating function of the form
to have a generating function of the form![]() where
where![]() is some well behaved function of
is some well behaved function of![]() and
and ![]()
The canonical transformation produced by this generating function is![]() (1)
(1)
![]() (2)
(2)
Since![]() we may substitute
we may substitute![]() for
for![]() on the right hand side of (2) to obtain
on the right hand side of (2) to obtain
![]()
![]()
where![]() called the generator of the infinitesimal canonical transformation.
called the generator of the infinitesimal canonical transformation.
The transformation is canonical to first order since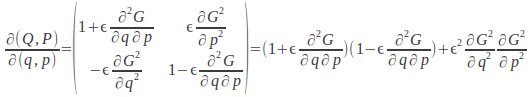
![]()