Introduction to Angle Action Variables
It is desirable to construct a coordinate system in which the Hamiltonian has the simplest possible form. In the case of rotational or librational motion one of those coordinates behaves like an angle and the conjugate variable is called the action – in fact it is only for rotational or librational motion that angle action variables are defined. The coordinates taken together are called angle action variables. Angle action variables are of fundamental importance in quantum mechanics, where they are used for example to model the radiation emitted from quantum systems.
Most Hamiltonians![]() for functions of both the generalised coordinate
for functions of both the generalised coordinate![]() and the conjugate momentum
and the conjugate momentum![]() so Hamilton's equations
so Hamilton's equations![]() are coupled together. Of course, for a free particle the Hamiltonian
are coupled together. Of course, for a free particle the Hamiltonian![]() is independent of
is independent of![]() The equations of motion are immediately solvable and give
The equations of motion are immediately solvable and give![]() where
where![]() is a constant.
is a constant.
Angle action variables generalise this so that a transformation![]() is found such that the Hamiltonian expressed in the new coordinates is independent of
is found such that the Hamiltonian expressed in the new coordinates is independent of![]() Hamilton's equations can be solved immediately in the new coordinate system and transformed back to express the solution in the original coordinates.
Hamilton's equations can be solved immediately in the new coordinate system and transformed back to express the solution in the original coordinates.
If the Hamiltonian system is conservative, then we can find a transformation![]() where
where![]() is the time and
is the time and![]() is the (constant) energy.
is the (constant) energy.![]() and
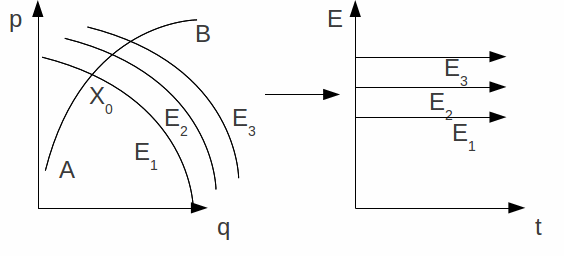
and![]() can be defined by choosing a phase curve, and a point on that curve, to be regarded as the initial point. The collection of initial points forms a curve AB at right angles to each phase curve and in the
can be defined by choosing a phase curve, and a point on that curve, to be regarded as the initial point. The collection of initial points forms a curve AB at right angles to each phase curve and in the![]() coordinates this will form the
coordinates this will form the![]() axis. The phase curve in the
axis. The phase curve in the![]() coordinates will be horizontal lines since
coordinates will be horizontal lines since![]()