A system influenced by time dependent forces or which is represented in a rotating or non inertial reference frame has a Hamiltonian which depends explicitly on time,![]() The rate of change of the Hamiltonian is given by
The rate of change of the Hamiltonian is given by
![]()
On using Hamilton's equations of motion this becomes
![]()
The value of the Hamiltonian is not conserved, however the area is.
Proof:![]() and
and![]() not necessarily Hamiltonian. At time
not necessarily Hamiltonian. At time![]() the area of a region of phase space is given by
the area of a region of phase space is given by![]() and at
and at![]()
As![]() increases from
increases from![]() to
to![]() a point
a point![]() in
in![]() is sent to a point
is sent to a point![]() in
in![]() so that
so that![]() can be considered as the initial condition on a trajectory
can be considered as the initial condition on a trajectory![]() where
where![]() and the transformation from
and the transformation from![]() to
to![]() is given by
is given by![]()
The area at time![]() is given by
is given by![]() where
where ![]() is the Jacobian matrix of the transformation.
is the Jacobian matrix of the transformation.
We can expand![]() and
and![]() in Taylor series:
in Taylor series:
![]()
![]()
Then the Jacobian can be written as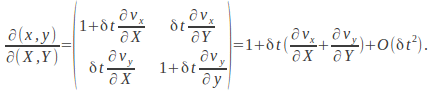
Consider![]()
![]()
Hence![]() on use of Hamilton's equations and area is preserved.
on use of Hamilton's equations and area is preserved.