\[R\]
and the length of the rod is \[l\]
. and we let the centre of the flywheel be the origin, then from the diagram below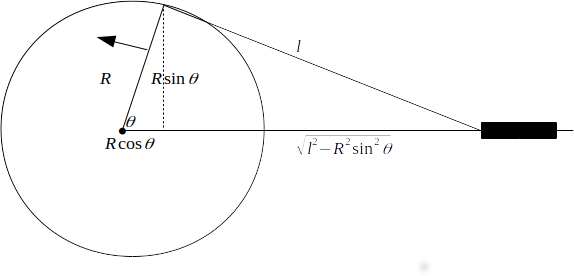
\[x=R cos \theta + \sqrt{l^2- R^2 sin^2 \theta}\]
.The velocity of the piston at any time is
\[v= \frac{dx}{dt}=-R \dot{\theta} sin \theta - \frac{R^2 \dot{\theta} cos \theta sin \theta }{\sqrt{l^2-R^2 sin^2 \theta}}\]
and the acceleration is
\[\begin{equation} \begin{aligned} a &= \frac{dv}{dt}=-R \ddot{\theta} sin \theta- R \dot{\theta}cos \theta \\ &- - \frac{R^2 \ddot{\theta} cos \theta sin \theta -R^2 \dot{\theta}^2 sin^2 \theta + R^2 \dot{\theta}^2 cos^2 \theta }{\sqrt{l^2-R^2 sin^2 \theta}} \\ &-\frac{R^4 \dot{\theta}^2 cos^2 \theta sin^2 \theta }{(l^2-R^2 sin^2 \theta )^{3/2}} \end{aligned} \end{equation}\]