Consider the steady, uniform flow of an inviscid, incompressible liquid in an open channel with a rectangular cross section of constant width. If the width is![]() and the depth is
and the depth is![]() the volume flow rate
the volume flow rate![]() where
where![]() is the speed of the liquid.
is the speed of the liquid.![]() is constant from the continuity equation, since the liquid does not accumulate in any part of the channel. If
is constant from the continuity equation, since the liquid does not accumulate in any part of the channel. If![]() is the volume flow rate per unit width then
is the volume flow rate per unit width then![]()
We apply Bernoulli's equation along a streamline in the free surface of the liquid in a flat bottomed channel, giving![]() where
where![]() is the atmospheric pressure, assumed constant. Since the density is also constant we can subtract
is the atmospheric pressure, assumed constant. Since the density is also constant we can subtract![]() from each side, giving
from each side, giving![]() Dividing by
Dividing by![]() gives
gives![]() where
where![]() is called the specific energy.
is called the specific energy.
If![]() is constant then
is constant then![]() so
so![]() or
or![]()
The last equation is a cubic in h, so may have 3 distinct real roots or one. If there are three roots for this particular equation, one of the roots is negative, so physically meaningless, so for given![]() and
and![]() there are either one or two possible values of
there are either one or two possible values of![]() There are three possible cases.
There are three possible cases.
-
If
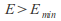 two flows are possible at different depths
two flows are possible at different depths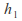 and
and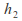 corresponding to speeds
corresponding to speeds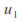 and
and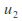 are possible.
are possible.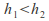 and since
and since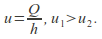 The first is described as shallow and fast or supercritical, the second as deep and slow or subcritical.
The first is described as shallow and fast or supercritical, the second as deep and slow or subcritical. -
If
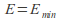 the flow is unique. The liquid flows with depth
the flow is unique. The liquid flows with depth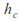 and speed
and speed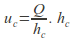 and
and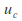 are the critical speed and critical depth respectively.
are the critical speed and critical depth respectively. -
If
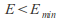 then no flow is possible.
then no flow is possible.
All the cases are illustrated below.
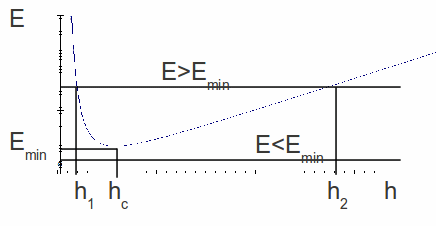
Since the critical depth![]() occurs at a minimum of the specific energy function, we can differentiate
occurs at a minimum of the specific energy function, we can differentiate![]() and equate to zero to find
and equate to zero to find![]()
![]()
The minimum value of the specific energy is then![]()