In one dimension the motion of a system may be described by a function of position and time satisfying the equation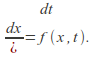
In general the velocity of the particle will be a function of time. If however
is actually independent of
then the position of the particle will depend only on the difference
since if
separation of variables gives
Integration now gives
Example: The equation of radioactive decay,
is an autonomous system. Separation of variables and integration gives
Rearrangement gives
The original equation implies that the probability of decay does not depend when the decay takes place. This is a vital property, used in radioactive dating.
In general all the solutions of an autonomous system are relation. If two solution are
and 
with
thenmust satisfy
The above discussion can be extended to higher order systems in the natural way.