Normalizing the Wavefunction
The Born interpretation gives the probability of finding a particle with wavefunction![]() - I have shown the wavefunction here to be a function of here, though I need not have done and do not use this below - in the volume of space between
- I have shown the wavefunction here to be a function of here, though I need not have done and do not use this below - in the volume of space between![]() and
and![]() is
is![]()
The particle must by definition be somewhere, so we can add up all the probabilities or integrate over the whole volume where the particle might be and this value must be equal to 1. This may be stated![]() (1)
(1)
This equation is so important because we may be able to find the form of the wavefunction by solving Schrodinger's equation, with the associated boundary conditions, But we can not know the size of the wavefunction using just the Schrodinger equation. This means that the wavefunction includes an arbitrary constant as a factor, and we evaluate this constant using equation (1). This process of finding the arbitrary factor associated with a wavefunction is called normalizing the wavefunction.
Example: The ground state wavefunction for an infinite square well in one dimension between![]() and
and![]() is given by
is given by![]() Find
Find![]()
![]()
In this case the 'volume' is the![]() – axis between
– axis between![]() and
and![]()
![]()
Use the identity![]()
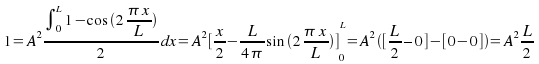
Hence![]() and
and![]()