The particles in a gas can move in three directions – up/down, backwards/forwards and left/right. We say the particles have three translational degrees of freedom because of the directions in which they can move in space. One third of the kinetic energy of the particles of the gas is associated with each direction. The kinetic energy of the 1 mol of particles of an ideal gas is given by![]() where
where ![]() is the Universal Molar Gas Constant, so each degree of freedom has
is the Universal Molar Gas Constant, so each degree of freedom has![]() joules of energy associated with it.
joules of energy associated with it.
For the particles of a monatomic gas, so that each gas particle is a single atom, the above discussion is complete. If the particles of a gas consist of more than one atom, the situation is more complex. The simplest cases is where the gas molecules are identical. If they consist of two atoms, the gas molecules may vibrate or rotate. We say the molecules have vibrational and rotational degrees of freedom. For normal temperatures, the energy of each vibrational degree of freedom is very low, but the energy associated with each rotational degree of freedom is the same as the energy associated with each translational degree of freedom. This is the principle of equipartition of energy. A molecule consisting of two atoms may rotate in two modes as shown below.
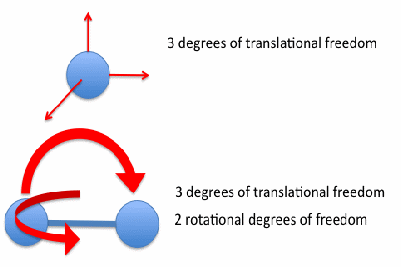
The energy of the one mol of the particles of a diatomic gas is then given by![]()
The relationship between the molar specific heat capacity of an ideal gas at constant pressure,![]() and the molar specific heat capacity at constant volume,
and the molar specific heat capacity at constant volume,![]() is
is![]() Defining
Defining![]() we have
we have![]() for a monotomic gas and
for a monotomic gas and![]() for a diatomic gas. More generally for an ideal gas with n degrees of freedom,
for a diatomic gas. More generally for an ideal gas with n degrees of freedom,![]()