Here we are concerned with lengths of arcs and areas of segment and sectors.
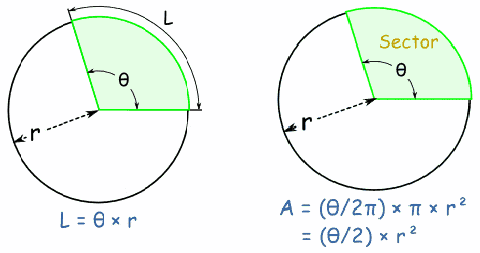
The circumference of a circle is 2%pi r. If we haven't got a whole circle or we want to find the length of just part of it's circumference, we find find the cicumference of just that part of the circle. The fraction we have got is {%theta} over {2%pi} – since we work in radians with circular measure.
Hence
The same logic can be used to find the formula for the area of a sector, illustrated above right.
These formulae may be used to answer the following questions.
Find the area of the segment shaded green below.
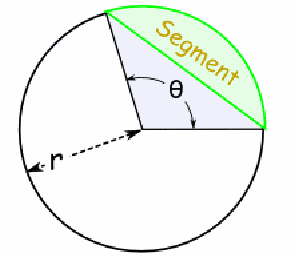
The area of the sector is
The area of the purple shaded triangle is
using the standard formula for the area of a triangle.
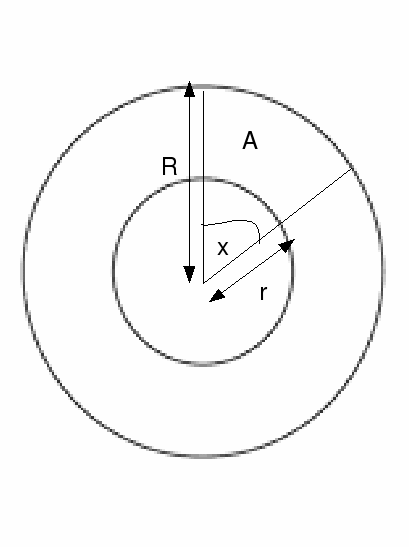
The area A is given by the formula
where
is in radians.. This is just the different between the area of the large sector with angleand the small sector with angle