A trapezium is isosceles if it has a line of symmetry, like the trapezium below.

If a trapezium is isosceles, when reflected in the line of symmetry, the slant heights must be reflected onto one another. This means they must have the same length, a given the endpoints of the lines.
\[(x_1,y_1), \: (x_2,y_2)\]
, we can find the length
\[d\]
using
\[d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\]
.
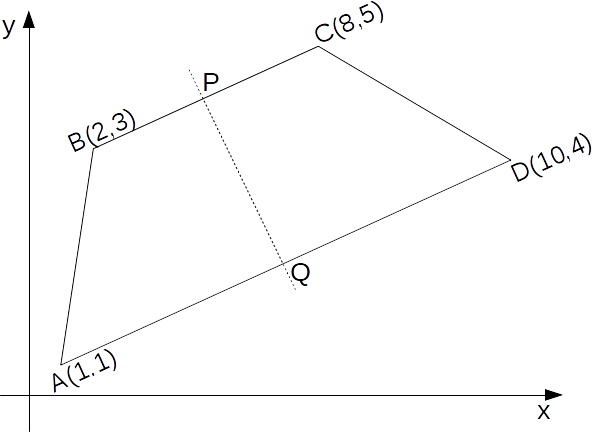
This distance from A to B is
\[|AB|= \sqrt{(2-1)^2+(3-1)^2}=\sqrt{5}\]
.
This distance from A to B is
\[|CD|= \sqrt{(10-8)^2+(4-5)^2}=\sqrt{5}\]
.
The distances are the same, and so the trapezium is isosceles.


