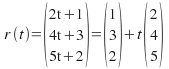Changing Between Cartesian and Vector Forms of Equations of Lines in Three Dimensions

You may be used to seeing the cartesian –– form of a line as something likeor but expressions like these are not possible in three dimensions. We go right back to the vector form, and start by identifying theandcomponents:

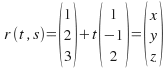
HenceFor each of these three components we make the parameter the subject:

Each of these expressions are equal toso they are all equal to each other:

This expression is the cartesian form of a line in three dimensions.

Conversely, given the cartesian form of a line we can write out down the vector form:

Each term is not constant sinceandare variables, so put them equal to a common parameterand write down separate equations for each component, solving them forand

Then