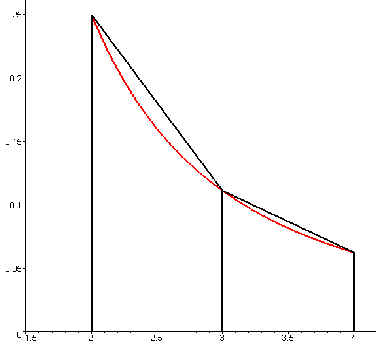
The trapezium rule is a numerical method for estimating integrals. It is most useful when there is no analytical answer to an integral, and only a number is needed. It works by approximating the area under the curve by a series of trapezia, then evaluating the areas and adding them up.
The area under the curve
is approximated by a series of trapezia.
The formula for the integral rule is
where
is the step size or the increment by which the values of
increases, 1 in the diagram above and
is defined by
eg
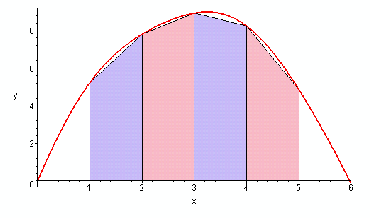
For ease of calculation it is a good idea to tabulate the values of the
|
i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
xi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
yi |
0 |
5 |
8 |
9 |
8 |
5 |
0 |
This estimate just calculated is an underestimate for the integral. The curve is concave – it curves down. In general the trapezium method gives an underesimate for concave integrals and an overestimate for convex integrals, an example of which is given below.
