Motion of Particle on Inner Surface of Smooth Sphere

A particle travelling on the inside surface of a smooth sphere will just leave the surface when the reaction between the particle and the inner surface is zero.

Suppose a particle of massat the bottom A of a sphere of radius r is given a horizontal speedIt will move along the internal surface of the sphere. Suppose at some point B it has a speed

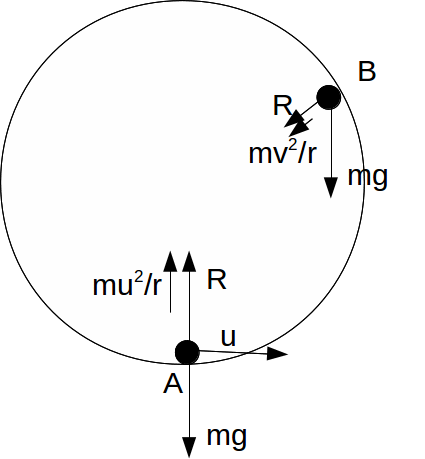
If the line from the centre of the circle to the point B makes an anglewith the upwards vertical then the force of gravity will have a componenttowards the centre of the circle.

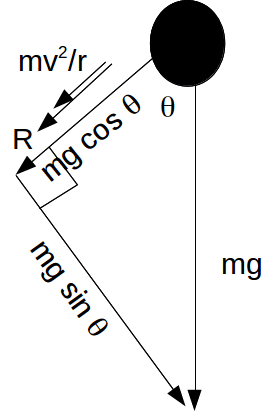
Applyingtowards the centre of the circle gives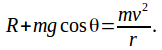 (1)

Since the inside of the sphere is smooth, no work is done against friction, and energy is conserved in going from A to B. The potential energy at B is

Hence

Cancellinggives (2)

Putin equation (1) and cancelfrom both sides, obtaining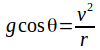thenSubstitute this into (2) to obtain

Rearranging this formula forgives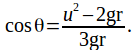

Sincewe must have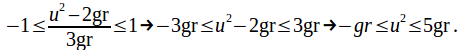

Obviously

The particle will leave the inside surface at some point ifThis corresponds to the particle not having enough initial kinetic energy to reach the top of the sphere.