Motion without friction is in most practical situations an unachievable ideal. There is always some friction and some work must always be done to overcome it.
If the friction force
is constant for a distance moved
then the work done to overcome that force is
We can obtain another very useful equation from this by differentiation.
is constant so
Consider the meaning of this equation. When a car is moviing at a velocity v on a level road, it is doing work at a rate Fv to overcome friction. The car engine can only supply power up to a certain maximum rate,
When the speed
is such that
the car cannot accelerate any more because to do so would require that some of the energy supplied by the car engine is used to increase the cars kinetic energy, which is impossible because all the power supplied by the engine is being used to overcome friction.
In general though, the power supplied by a car is used up in several ways. It can be used to drive the car uphill (if the car is driving downhill, this energy is changes sign), increase the kinetic energy and speed, or overcome friction. We write
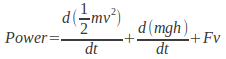
Assuming
to be constant (in fact the car is losing mass because fuel is being burnt), we can write
We can use the chain rule to simplify
obtaining
hence
Finally, there is a relationship between
and
Assume the slope is at an angle
to the horizontal then from the diagram below
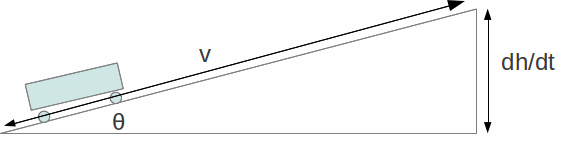
Hence we can write