The Work Energy Principle for a Particle Attached to an Elastic String on a Rough Slope

The Work Energy Principle states that for an isolated system, as the system proceeds to evolve, the difference between the initial energy and the energy at any instant has been used to overcome air resistance or friction of some sort.

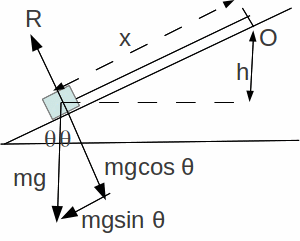
Consider a particle of masson a rough slope. The coefficient of friction between the particle and the slope isInitially the particle is at some point O on the slope and with pushed directly down the slope with a speed

We can take the gravitational potential energy of the particle relative to O.

InitiallySince the particle is below O, the gravitational potential energy is always less than or equal to zero. Initially the string is unstretched so has elastic potential energy zero.

Initially the kinetic energy is

At any subsequent time, the gravitational potential energy ithe kinetic energy isIf the natural length of the string is l then the extension for x the extension isand the stored elastic potential energy is

The reaction force(resolving perpendicular to the slope in the diagram above) so the force of frictionIn moving a distance the work done against friction is

At any time the work energy principle states:

for

for