All bodies lose and gain thermal energy by means of electromagnetic radiation. The rate of energy loss depends on the temperature of the body. Stefan's Law states that the power radiated by a body – it's luminosity - is proportional to the 4th power of the absolute temperature T. Thus
![]() (1)
(1)
where![]() is the emissivity of the surface of the body,
is the emissivity of the surface of the body,![]() is the Stefan-Boltzmann constant equal to
is the Stefan-Boltzmann constant equal to![]() and
and![]() is the surface area of the body. The value of the emissivity is between zero and one, and equals one for a perfect black body. Bodies can, of course, lose heat by other mechanisms (conduction and convection), but at high temperature radiation becomes dominant. If we assume we are analysing the radiation from a black body – often a good approximation – then we can write (1) as
is the surface area of the body. The value of the emissivity is between zero and one, and equals one for a perfect black body. Bodies can, of course, lose heat by other mechanisms (conduction and convection), but at high temperature radiation becomes dominant. If we assume we are analysing the radiation from a black body – often a good approximation – then we can write (1) as
![]()
Suppose we are analysing the light from a star. If we assume the star to be spherical then![]() and we can write
and we can write![]() (2)
(2)
This formula allows us to estimate the radii of stars. We can estimate the temperature using Wien's Law. Finding the luminosity might appear to be a problem given that a star is presented to us as just a point of light, and for virtually all stars we cannot measure the radius. How there is a solution. In the early years of the Twentieth Century, astronomers compared the spectra of stars with different luminosities but similar temperatures. They found that, at a given temperature, the more luminous the star, the narrower it spectral absorption lines, and the stronger are the absorption lines due to certain ionized ions. As shown below, there is is also a dependence of the width of the lines on the density of the star in the region of emission and the type of star.
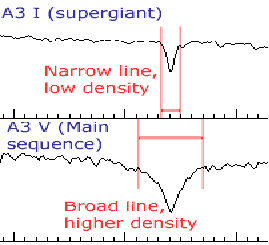
Hence we can estimate the luminosity of a star from the width of it's spectral lines, the temperature of a star from Wien's Law and then use Stefan's Law to find the radius of the star.
