If the balls are replaced each time after they are picked, the probability of picking a ball of a particular colour never changes. Before each pick there are always three red balls and two blue balls in the bag.
If the balls are not replaced each time after they are picked, the probability of picking a ball of a particular colour changes. If a blue ball is picked, there is one less blue ball in the bag, so the probability of picking a blue ball again is less.
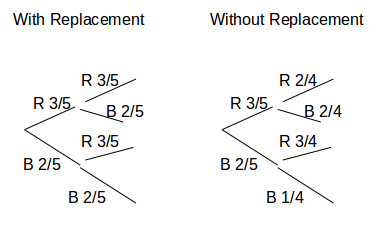
Probability of picking two red balls
\[P(RR)=\frac{3}{5} \times \frac{3}{5}=\frac{9}{25}\]
Probability of picking a red ball then a blue ball
\[P(RB)=\frac{3}{5} \times \frac{2}{5}=\frac{6}{25}\]
Probability of picking a blue ball then a red ball
\[P(BR)=\frac{2}{5} \times \frac{3}{5}=\frac{6}{25}\]
Probability of picking two blue balls
\[P(BB)=\frac{2}{5} \times \frac{2}{5}=\frac{4}{25}\]
Without Replacement:
Probability of picking two red balls
\[P(RR)=\frac{3}{5} \times \frac{2}{4}=\frac{6}{20}\]
Probability of picking a red ball then a blue ball
\[P(RB)=\frac{3}{5} \times \frac{2}{4}=\frac{6}{20}\]
Probability of picking a blue ball then a red ball
\[P(BR)=\frac{2}{5} \times \frac{3}{4}=\frac{6}{20}\]
Probability of picking two blue balls
\[P(BB)=\frac{2}{5} \times \frac{1}{4}=\frac{2}{20}\]
