Estimating Uncertainty

An uncertainty range applies to any experimentally found value. Instead of giving one value that implies (incorrectly) precision, we give an interval for the measurement that includes a range of likely values.All measurements involve an error made in merely taking the reading. If we use a measuring cylinder to find the volume of a liquid, we might estimate the volume of liquid indicated below as 250 ml, but we could not be confident of it being 250.0000000ml (to seven decimal places).

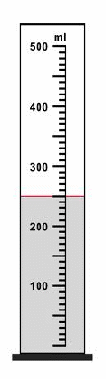
Normally the uncertainty range to to reading errors is given as below.

We can estimate the uncertainty given several measurements. For example, given the five measurements 2.01, 1.82, 1.97, 2.16 and 1.94 seconds respectively, the average is 1.98 seconds. The difference between the average and the smallest reading (1.98-1.82=0.16 seconds) and the difference between the average and the largest reading (2.16-1.98=0.18 seconds)is found and the largest of these values is taken to be the uncertainty. It this case the uncertainty is 0.18 seconds and the uncertainty range isseconds.