We use moments when an object might be made to turn about a point. We can work out which direction it will turn in. Moments are very useful however for working out unknown forces or distances, if the system in question is in equilibrium, so that
Sum of Clockwise Moments = Sum of Anticlockwise Moments
Example: Suppose we want to work out the force F below for the system in equilibrium.
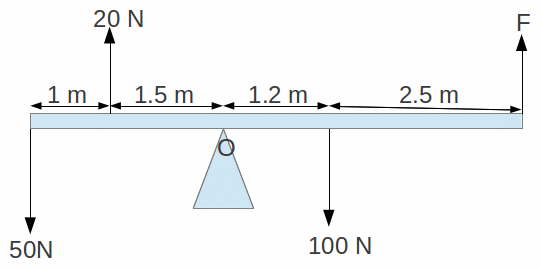
The pivot or balance point is O so it is natural to take moments about O. We can draw up the following table.
|
Force/N |
Distance From O/m |
Force Times Distance/N m |
Clockwise or Anticlockwise |
|
50 |
2.5 |
125 |
Anticlockwise |
|
20 |
1.5 |
30 |
Clockwise |
|
100 |
1.2 |
120 |
Clockwise |
|
F |
3.7 |
3.7 F |
Anticlockwise |
The sum of the clockwise moments is 150 Nm and the sum of the anticlockwise moments is 125+3.7 F Nm. Equating these gives
![]() to 2 decimal places.
to 2 decimal places.
Example: We want to find x in the diagram below for the system in equilibrium. As before, O labels the balance or pivot point so we take moments about O.
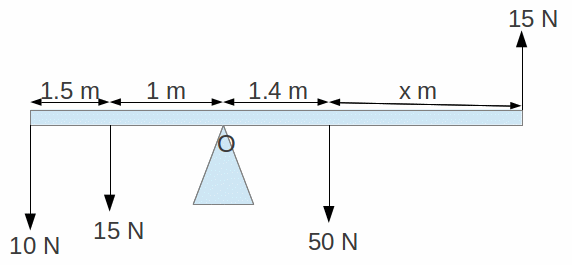
The table is
|
Force/N |
Distance from O/m |
Force times Distance/Nm |
Clockwise or Anticlockwise |
|
10 |
2.5 |
25 |
Anticlockwise |
|
15 |
1 |
15 |
Anticlockwise |
|
50 |
1.4 |
70 |
Clockwise |
|
15 |
1.4+x |
21+15x |
Anticlockwise |
The sum of the clockwise moments is 70 Nm and the sum of the anticlockwise moments is 25+15+21+15x=61+15x Nm. Equating these gives
![]()
