Consider the triangle below, with
\[\mathbf{AB}=\mathbf{b}, \; \mathbf{AC}= \mathbf{c}\]
and \[P, \; Q\]
as the midpoints of \[BC, \; AC\]
respectively.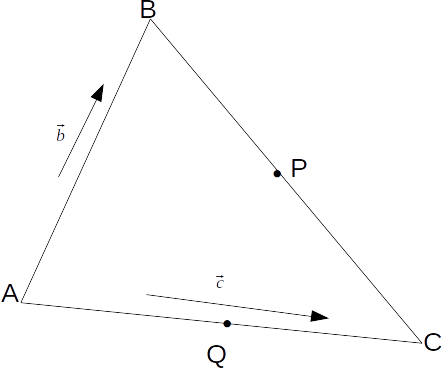
\[\mathbf{BC}= - \mathbf{b}+ \mathbf{c} \rightarrow \mathbf{BP}= \frac{1}{2}(- \mathbf{b}+ \mathbf{c})\]
.The equation of the line
\[BQ\]
is \[\mathbf{b}+ (- \mathbf{b}+ \frac{\mathbf{c}})s=(1-s) \mathbf{b}+ \frac{s}{2} \mathbf{c}\]
.The equation of the line
\[AP\]
is \[(\mathbf{b} + \mathbf{c}{2})t= \frac{t}{2} \mathbf{b} + \frac{t}{2} \mathbf{c}\]
(remembering that \[\mathbf{b}, \; \mathbf{c}\]
form a parallelogram, of which the triangle forms a half.Equating the coefficients of
\[\mathbf{b}, \; \mathbf{c}\]
to find the intersection gives\[1-s= \frac{t}{2}\]
\[\frac{s}{2}= \frac{t}{2}\]
From the second
\[s=t\]
and from the first \[s=t= \frac{2}{3}\]
. 