Kelvin's circulation theorem states: In an inviscid, barotropic flow with conservative body forces, the circulation around a closed curve moving with the fluid remains constant.
where
is the circulation around a material contour
which may vary with time and through which no material may pass. Stated more simply this theorem says that if one observes a closed contour at one instant, and follows the contour over time (by following the motion of all of its fluid elements), the circulation over the two locations of this contour are equal.
Kelvin's theorem ignores viscosity, friction, external rotation (coriolis) forces, all non conservative, and non-barotropic pressure-density relations.
Proof: The circulationaround a closed material contour
is defined by:
where
is the velocity vector, and
is an element along the closed contour.
The governing equation for an inviscid fluid with a conservative body force is
where
is the convective derivative,
is the fluid density,
is the pressure and
is the potential for the body force. These are the Euler equations with a body force.
The condition of barotropicity implies that the density is a function only of the pressure, i.e.
Taking the time derivative of circulation gives
For the first term, we substitute from the governing equation, and then apply Stokes' theorem, thus:
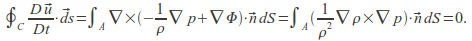
- The barotropicity condition means
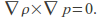
For the second term, we note that evolution of the material line element is given by
Hence
The last equality is obtained by applying Stokes theorem.
Since both terms are zero, we obtain the result