Viscosity may be thought of as a fluids resistance to the shearing forces acting on the fluid. We may picture a fluid between two plates, one stationary and one moving parallel to the first.

The relative motion of the two plates cause shearing forces on the liquid, deforming it. More viscous fluids offer more resistance to the shearing forces.
It the shear stress is proportional to the rate of deformation (1), the fluid is said to be Newtonian.
To derive an expression for the coefficient of viscosity, we assume the fluid above is incompressible.
The fluid moves in the x direction only so the continuity equation for an incompressible fluid,![]() gives
gives![]() For infinite plates the will be no
For infinite plates the will be no![]() dependence so
dependence so![]() so the speed in the
so the speed in the![]() – direction is a function of
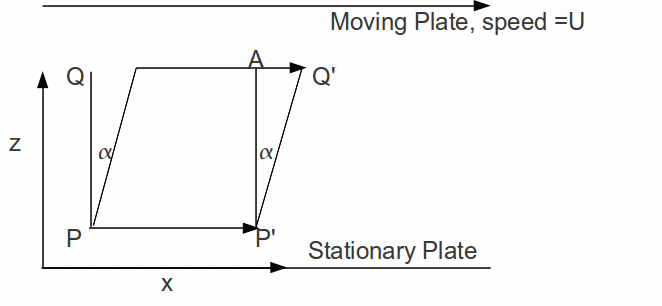
– direction is a function of![]() only. Let P and Q have coordinates
only. Let P and Q have coordinates![]() and
and ![]() let the speed at P be
let the speed at P be![]() and the the speed at Q be
and the the speed at Q be![]() In time
In time![]() the fluid particles at points P and Q have moved to P' and Q' respectively so that P'Q' is PQ deformed and the angle
the fluid particles at points P and Q have moved to P' and Q' respectively so that P'Q' is PQ deformed and the angle![]() measures the deformation. To a first approximation
measures the deformation. To a first approximation![]()
The rate of deformation of the fluid is then![]() (2). If we label the stress by
(2). If we label the stress by![]() we can use (1) to write
we can use (1) to write![]() where
where![]() is the constant of proportionality called the coefficient of viscosity. Then from (2)
is the constant of proportionality called the coefficient of viscosity. Then from (2)![]()
