The classical definition of angular momentum is
The result is a vector, perpendicular to both vec r and vec p . Angular momentum is so important because it is conserved in any isolated system. The same relationship, (1) holds in quantum mechanics, with
and
being the position and momentum operators respectively:
can be evaluated as the determinant of a matrix, the first row of which consists of the unit vectors
the second row of the components of the position operator, and the third row of the components of the momentum operator. We expand along the top row.
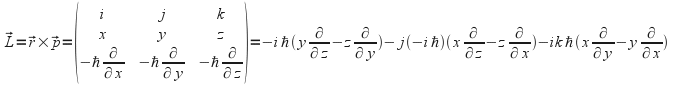
All the coefficients are by convention written as positive. We can do this by taking the negative sign belonging to the first and last terms inside the brackets, obtaining
This is the most general form of the angular momentum operator. We can separate this into it's components:
The operators can also be written with respect to and angle. This is common for
often written