Properties of the Eigenfunctions

The eigenfunctionsare the solutions of the eigenfunction equationthe solutionsfor the one dimensional simple harmonic oscillator case, are polynomials inmultiplied by a gaussianIf theare normalized to unity they have the following properties:

1. The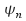are orthonormal This means that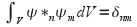(1) where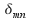is the Kronecker delta, defined by

2. The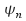form an abstract vector space. Any arbitrary wavefunction can be expressed in terms of the eigenfunctions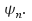We can write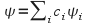(2) or using the abstract vector space properties of the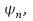we can write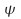as a column vector:

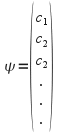with the property that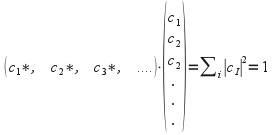

In this expression theare the coefficients of the eqienfunctions in the expression (2), and the position in the ith row signifies the ith eigenvector. It must be understood here that the vector space usually has infinite dimension. Because we can write the wavefunction as a column vector, we can operate on it with a matrix like any other vector.

3. For the one dimensional case, asThis is necessary so that the eigenfunction can be normalized.

4. is real for the one dimensional harmonic oscillator,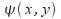is real for the two dimensional harmonic oscillator and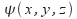is real for the three dimnsional harmonic oscillator.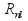is real for the hydrogen atom, and in fact for all stationary state eigenfunctions. Each of these may be multiplied by a time term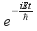and in the case of the hydrogen atom, an angular term which is complex in general, to obtain the state function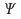which is a function of t and other space variables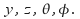Each of these factors is normalised to 1.

5. Given a wavefunction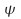we can find the coefficients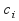using that all the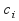are orthogonal.

Take the dot product with

sincebeing normalized, hence

The dot product here is the generalized dot product – it could be an integral for example as in (1).