When a particle represented by a wavefunction hits a potential barrier, it is not automatically relected, even if it has insufficient energy to over come the barrier according to classical mechanics. If the potential barrier has finite height, the wavefunction partially penetrates the barrier. If the barrier has finite extent, then at the other side of the barrier the wavefunction may not be identically zero. The diagram below shows a particle incident from the left to hit the barrier at x=0, and partially emerge on the other side at x=L
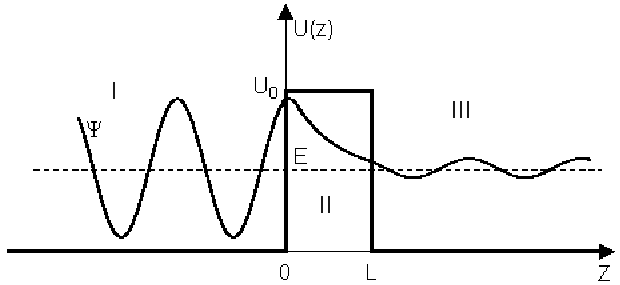
We can find the probability of the particle being reflected – the reflection coefficient – and absorped – the absorption coefficient. Since Schrodinger's equation is second order, %psi and {d %psi} over {d x} are continuos everywhere and we can equate them at x=0 and x=L, form simultaneous equations and solve them for the coefficients.
In region I,
where
In region II
where
In region III,
where
since
in I and III.
At
and
(1)
(2)
At
and
(3)
(4)
The reflection coefficient is