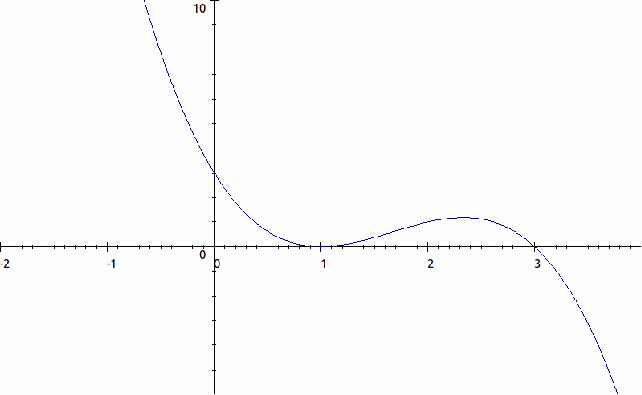Curve Sketching

When sketching curves of a polynomial function

1. try to factorise it first, if it is not already factorised. Writing a polynomial as a product of factors -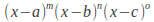- for example - makes it easier to identify the roots – the points where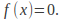The roots will be points on the x – axis, since each root is a solution of the equation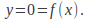

2. Find the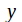– intercept by substituting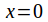into

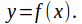
3. Decide whether the curve tends to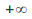or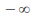as x tends to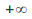or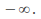If the coefficient of the highest power of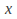is positive when the expression is expanded, then as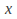tends to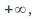so does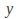and if the coefficient is negative, then as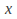tends to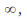 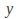tends to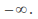

4. Each distinct root -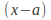- with no power - will give rise to a point on the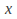– axis where the curve CROSSES the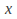– axis, and each repeated root - given by a factor – will give rise to a point on the curve which touches the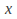– axis but does not cross it if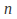is even, or which forms a tangent to the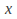– axis and crosses it if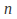is odd. Examples are shown below.

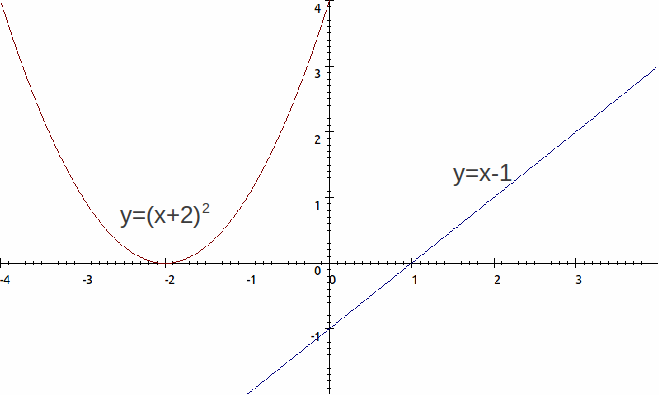
For example, to sketch

The roots are the solutions to

These are

Substitutinginto the expression gives

The highest power ofisand the coefficient ofis 2 (considersoas

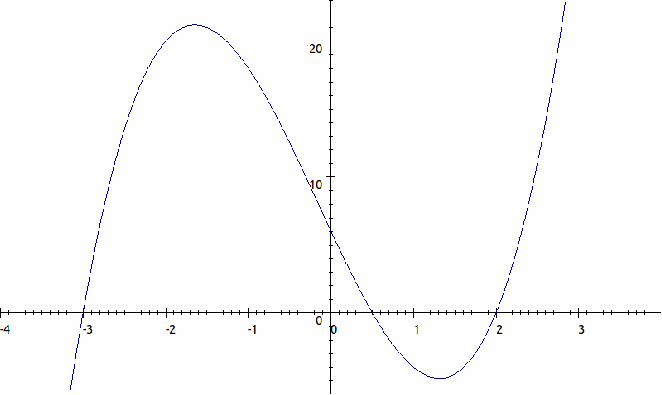
Each root is distinct, so the graph crosses the– axis at each root. The graph is sketch below.

To sketch

The roots are given by

Substitutinginto the expression gives

The highest power ofisand the coefficient ofis -1 (considersoas

The root atis a double root, so the curve touches theaxis atbut does not cross it, and the root atis a single root so the graph crosses the– axis there.

The curve is sketched below.