To solve the equation
could turn out to be quite a tricky problem. To solve exactly you may have to factorise the cubic equation
There is a simple to solve the inequality approximately. You can sketch the curve
and find those
values for which
This will be the solution set of the inequality. The points to be plotted are shown in the table below.
|
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
-27 |
-8 |
-1 |
0 |
1 |
8 |
27 |
|
|
-9 |
-4 |
-1 |
0 |
-1 |
-4 |
-9 |
|
|
15 |
10 |
5 |
0 |
-5 |
-10 |
-15 |
|
|
-21 |
-2 |
3 |
0 |
-6 |
-6 |
3 |
The curve is sketched below.
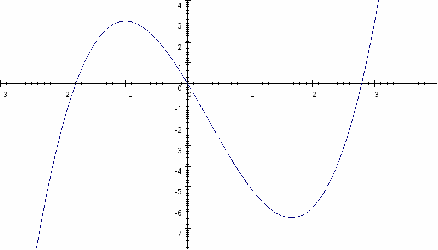
To solve the inequality we find the intersection of the curve with the line
and read off the – values for those points of intersection.
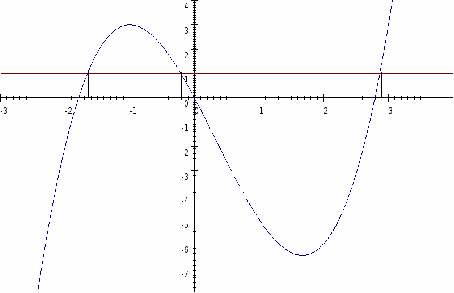
The lineintersects the curve at the points where
and
The curve is less than, or below the linefor
and