\[x\]
. We can find \[x\]
using simple trigonometry. Consider the triangle below.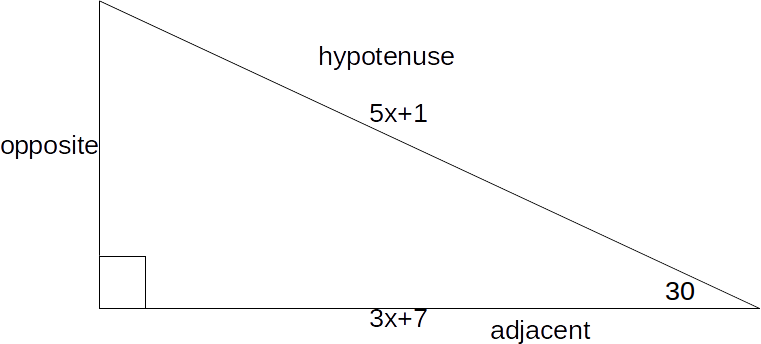
\[cos 30 = \frac{adjacent}{hypotenuse}\]
\[\frac{\sqrt{3}}{2} = \frac{3x+7}{5x+1}\]
\[\sqrt{3} (5x+1) = 2(3x+7)\]
\[5x \sqrt{3}+ \sqrt{3} = 6x+14\]
\[5x \sqrt{3}-6x = 14- \sqrt{3}\]
\[x(5 \sqrt{3}-6) = 14- \sqrt{3}\]
\[x = \frac{14- \sqrt{3}}{5 \sqrt{3}-6}= \frac{14- \sqrt{3}}{5 \sqrt{3}-6} \times \frac{5 \sqrt{3}+6}{5 \sqrt{3}+6}= \frac{69 +64 \sqrt{3}}{39}\]
