Solution: Draw a rectangle with longer side
\[l\]
and shorter side \[s\]
. Draw a diagonal \[AC\]
then the crease \[PQ\]
must bisect this crease at right angles.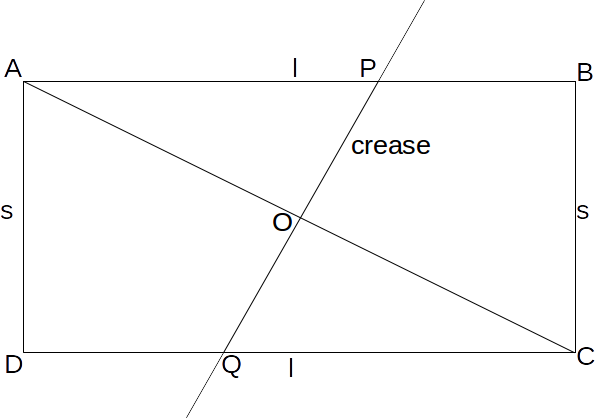
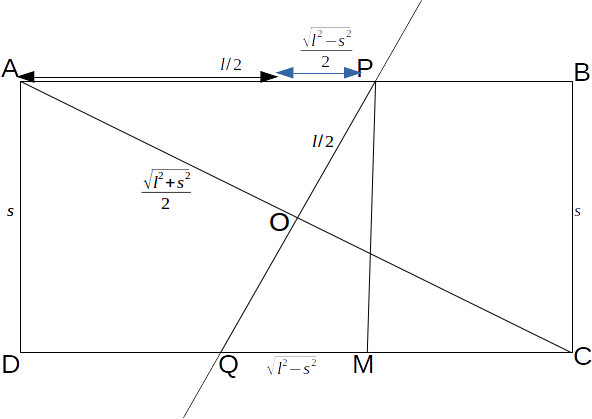
\[AC\]
is \[\sqrt{l^2-s^2}\]
by Pythagoras Theorem and the distance \[AO\]
is half of this: \[AO= \frac{\sqrt{l^2+s^2}}{2}\]
Also since the crease
\[PQ\]
is of length \[l\]
and the diagonal bisects the crease, \[OP=\frac{l}{2}\]
\[AOP\]
is a right angled triangle since \[PQ\]
bisects \[AC\]
at right angles. We can find two expressions for \[AP\]
and equate them.Drop a perpendicular from P to the base of the rectangle then
\[PMQ\]
is a right angled triangle and \[PM=s\]
.By Pythagoras Theorem
\[QM= \sqrt{l^2 - s^2}\]
and \[PO\]
is half of this: \[PM=\frac{\sqrt{l^2-s^2}}{2}\]
.
\[AOP\]
.\[ ( \frac{l}{2} + \frac{\sqrt{l^2-s^2}}{2})^2 = (\frac{l}{2})^2 + (\frac{\sqrt{l^2+s^2}}{2})^2\]
\[\frac{l^2}{4} + \frac{l \sqrt{l^2-s^2}}{2} +\frac{l^2-s^2}{4}=\frac{l^2}{4} + \frac{l^2+s^2}{4} \]
\[\frac{l \sqrt{l^2-s^2}}{2}= \frac{s^2}{2}\]
\[l^2(l^2-s^2) =s^4\]
\[ l^4-l^2s^2-s^4=0\]
We can treat this as a quadratic in
\[l^2\]
with solutions \[l^2 = \frac{s^2 \pm \sqrt{s^2+4s^2}}{2} = s^2 (\frac{1 \pm \sqrt{5}}{2}) \]
We only need the positive option since the negative one mean
\[l^2\]
is negative.Hence
\[l= s \sqrt{\frac{1+ \sqrt{5}}{2}}\]
