Finding Equations of Lines in Canonical Form

One of the most useful forms of the equation of a flat surface isWe have to be able to write the equations of lines in this form. We may have to do this in various ways.

1. We are given two points:

Find the line which passes throughand

The gradient of the line is

1. We are told a point on the line and the gradient of the line.

Find the equation of the line with gradient 5 which passes through (6,7).

2. We are told two perpendicular lines meet at a given point or a given value of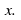Given the equation of one of the lines, find the equation of the other line.

A line meets the lineat right angles at the point P whose– coordinate is 2. Find the equation of the first line.

The y – coordinate ofis

The gradient of the line is -2 so the gradient of the perpendicular line is

3. We are told a line is parallel to some given line and passes through some point.

The line l is parallel toand passes throughFind the equation of

Since the lines are parallel the gradient