If a curve is sloping up![]() is positive. and if a curve is sloping down then
is positive. and if a curve is sloping down then![]() is negative
is negative
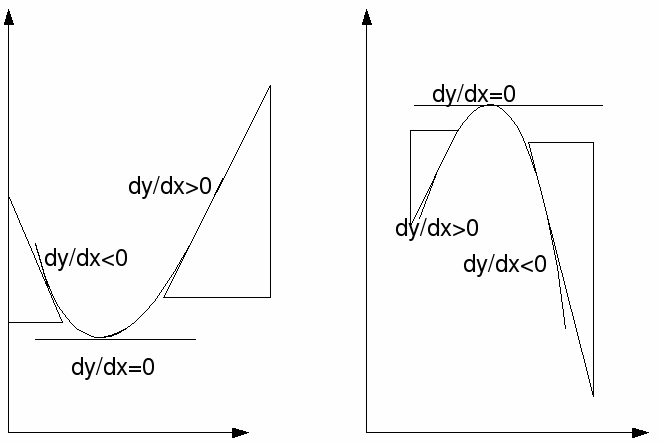
The graph on the left has![]() increasing – it goes from negative to zero to positive. This means that the gradient of
increasing – it goes from negative to zero to positive. This means that the gradient of![]() is positive.
is positive.
The graph on the right has![]() decreasing – it goes from positive to zero to negative. This means that the gradient of
decreasing – it goes from positive to zero to negative. This means that the gradient of![]() is negative.
is negative.
In both cases at the actual turning point (maximum or minimum) the gradient![]() is zero. To find and classify the turning points we first differentiate and set
is zero. To find and classify the turning points we first differentiate and set![]() equal to zero. We solve this equation to find the x values of the turning points, then differentiate
equal to zero. We solve this equation to find the x values of the turning points, then differentiate![]() to find
to find![]() and put the
and put the![]() values we have found into this expression. If the value we obtain here is positive then we have found a minimum for
values we have found into this expression. If the value we obtain here is positive then we have found a minimum for![]() If the value we obtain is negative then we have found a maximum for
If the value we obtain is negative then we have found a maximum for![]() If we need to find the
If we need to find the![]() – coordinate too we can substitute the
– coordinate too we can substitute the![]() – values of the minimum into the original expression for
– values of the minimum into the original expression for![]()
To summarise:
To find a turning point solve for![]()
![]()
To classify a turning point, put the![]() values of the turning point into the expression for
values of the turning point into the expression for![]()
If this value is positive, we have a minimum, and if it is negative we have a maximum. To find the![]() – value of the turning point, substitute the
– value of the turning point, substitute the![]() – values of the turning point into the expression for
– values of the turning point into the expression for![]()
Example. Find and classify the turning points of![]()
Solve![]()
![]() so the coordinates of the turning point are
so the coordinates of the turning point are![]()
![]() Therefore this is a minimum.
Therefore this is a minimum.
Example. Find and classify the turning points of![]()
Solve![]()
![]()
When![]()
When![]()
At![]() therefore this is a minimum.
therefore this is a minimum.
At![]() therefore this is a maximum.
therefore this is a maximum.
