A geometric series is such that each term is multiplied by a fixed number to get the next term.
1, 2, 4, 8, 16...
is a geometric series because each term is multiplied by a number called the common ratio – in this case 2, to get the next term. We may write
We can find a closed form expression for the n th term. If the first term is
and the common ratio is
the second term will be
and the third term will be
the fourth term
In general the nth term will be
We may also find an expression for the sum of a series up to n terms:
(1)
(2)
(1)-(2) gives
since all the other terms canel.
We can factorise both sides to give
If
then we may sum an infinite number of terms and obtain a proper answer, since in the expression for
above,
for
Hence
for
The formulae above may be used in the following ways:
The 1 st term of a geometric series is 4 and the 4 th term is 0.0625. Find
a) The sum of the series to infinity.
b)The least value of n such that the difference betweenand
is less than
a) 1 st term is
4 th term is
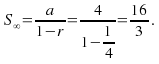
b)
Sub
to give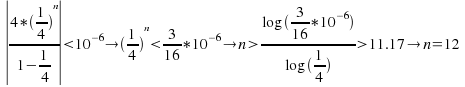
since
is a whole number.