\[x\]
axis and the tangent to the circle in the diagram, draw a line from the origin to the centre of the circle, a line from the centre of the circle to the \[x\]
axis, and a radius from the centre of the circle to the tangent.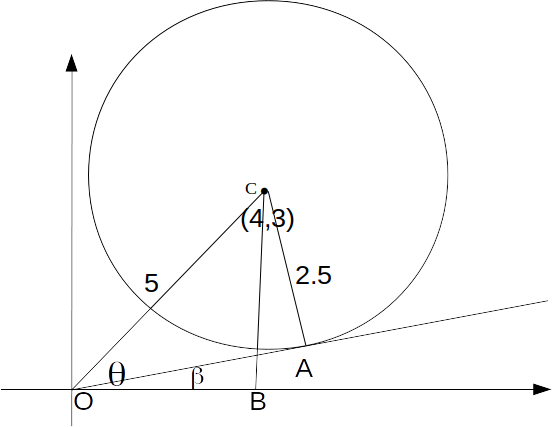
\[\theta = tan^{-1} ( \frac{4}{3} )\]
and \[\theta - \beta = sin^{-1} ( \frac{2.5}{5} ) \]
then \[\beta = \theta - (\theta - \beta ) = tan^{-1} ( \frac{4}{3} )- sin^{-1} ( \frac{2.5}{5} )=23.13^o \]
