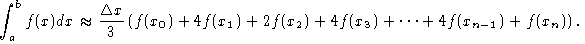Simpson's Rule is used to numerically estimate the value of integrals that either cannot be or are difficult to evaluate analytically. The rule approximates a function with a collection of arcs from quadratic functions and integrate across each of these.
Proof: Let P be a partition of [ a , b ] into n subintervals of equal width,
, where
for
. Here we require that
be even. Over each interval
, for
, we approximate f ( x ) with a quadratic curve that interpolates the points
, 
, and
.
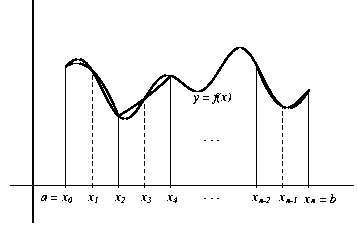
Figure 4:
Approximating the graph of y = f(x) with parabolic arcs across successive pairs of intervals to obtain Simpson's Rule.
Since only one quadratic function can interpolate any three (non-colinear) points, we see that the approximating function must be unique for each interval. Note that the following quadratic function interpolates the three points, , and:
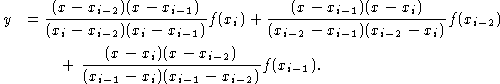
Since this function is unique, this must be the quadratic function with which we approximate f ( x ) on. Also, if the three interpolating points all lie on the same line, then this function reduces to a linear function. Therefore, since
for each i ,
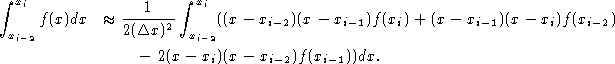
By evaluating the integral on the right, we obtain
Summing the definite integrals over each interval, for, provides the approximation
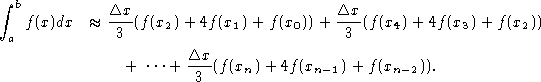
By simplifying this sum we obtain the approximation.
