An algebraic fraction is any expression of the form
where
and
are sums or products of polynomials or both. An expression of this sort typically needs to be written in terms of it's partial fractions – whereis written as a sum of algebraic fractions - so that it can be integrated. There are rules which determine which sums of fractions are allowable.
1. If the degree of the numerator is greater than or equal to the degree of the denominator, then first perform long division ofto reduce the degree of the polynomialto below that of
2. Factorise
as far as possible. Each factor
gives rise to a partial factor
3. Each factor
gives rise to a sum of partial fractions
4. Each irreducible factor
gives rise to a partial fraction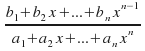
- notice that the degree of the numerator is one less than the degree of the denominator.
Example: Express
as partial fractions.
Example: Express
as partial fractions.
Example: Express
as partial fractions.
