To expand the expression
if n is a non negative integer, we can use Pascal's Triangle or the formula formula for the binomial expansion,
We can only use the formula above if
is a non negative integer. Ifis negative or a fraction we can still expand the expression, but must use the formula for the general binomial expansion:
The expansion is infinite, and in practice only a finite number of terms are found.
Example: Expand
up to and including the term in
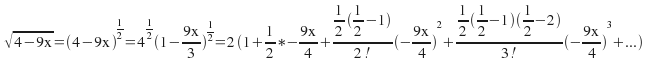
Simplifying the constant for each term gives
For each general binomial expansion of the type give above,
must be restricted to a certain interval, called the interval of convergence. For the the example above
It is no coincidence that
is then positive, since we are taking the square root of this expression in this question.
Example: Find the binomial expansion of
up to and including the term in
Simplifying the constant for each term gives
The above expansion is only valid for