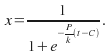The Logistic Equation

The equation takes a certain form and is used in many models, including the spread of diseases, discussed here. It is based on two assumptions

1. Since each infected person is capable of passing on the disease, the rate of spread of the disease is proportional to the infected population

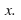
2. Since the disease may only be transmitted to uninfected people, the rate of spread of the disease is proportional to the number of uninfected people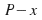where P is the total population.

Hence the rate of spread of the disease is proportional to the product of these two:

We separate the variables to obtainand then separate into partial fractions.

Multiply by x(P-x), clearing all the fractions, to obtain

hence We integrate:

The general solution of the logistic equation is given by t={k over P}ln({x over {P-x}) +C. This equation will give the time for any know population x. We can rearrange it to make x the subject:

We remove the ln by exponentiating both sides:

Now clear the fraction by multiplying by P-x to obtain

Now divide by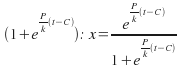

The final, possibly unnecessary step is to multiply numerator and denominator byto give